Trong hình 4.39, số đo góc BAC cũng được gọi là số đo góc giữa hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \). Hãy tìm số đo các góc giữa \(\overrightarrow {BC} \) và \(\overrightarrow {BD} \), \(\overrightarrow {DA} \) và \(\overrightarrow {DB} \).



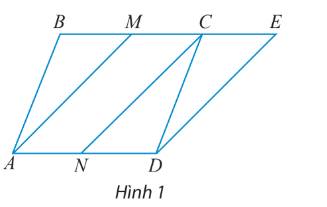
Góc giữa hai vectơ \(\overrightarrow {BC} \) và \(\overrightarrow {BD} \) là góc CBD và số đo \(\widehat {CBD} = {30^o}\).
Góc giữa hai vectơ \(\overrightarrow {DA} \) và \(\overrightarrow {DB} \) là góc ADB.
Ta có: \(\widehat {ACB} = \widehat {CBD} + \widehat {CDB}\) (tính chất góc ngoài)
\(\begin{array}{l} \Leftrightarrow \widehat {CDB} = {80^o} - {30^o} = {50^o}\\ \Leftrightarrow \widehat {ADB} = {50^o}\end{array}\)
Vậy số đo góc giữa hai vectơ \(\overrightarrow {BC} \) và \(\overrightarrow {BD} \), \(\overrightarrow {DA} \) và \(\overrightarrow {DB} \) lần lượt là \({30^o},{50^o}\)