Question

[Quoc Tran Anh Le]

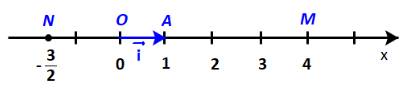
Trên trục số Ox, gọi A là điểm biểu diễn số 1 và đặt \(\overrightarrow {OA}  = \overrightarrow i \) (H.4.32a). Gọi M là điểm biểu diễn số 4, N là điểm biểu diễn số \( - \frac{3}{2}\). Hãy biểu thị mỗi vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) theo vectơ \(\overrightarrow i \).

Answer 1

[Hà Quang Minh]

Dễ thấy:

vectơ \(\overrightarrow {OM} \) cùng hướng với vectơ \(\overrightarrow i \) và \(\left| {\overrightarrow {OM} } \right| = 4 = 4\left| {\overrightarrow i } \right|\)

Do đó: \(\overrightarrow {OM}  = 4\,.\,\overrightarrow i \)

Tương tự, vectơ \(\overrightarrow {ON} \) ngược hướng với vectơ \(\overrightarrow i \) và \(\left| {\overrightarrow {ON} } \right| = \frac{3}{2} = \frac{3}{2}\left| {\overrightarrow i } \right|\)

Do đó: \(\overrightarrow {ON}  =  - \frac{3}{2}\,.\,\overrightarrow i \)