Cho hình vuông ABCD có hai đường chéo cắt nhau tại O. Hãy chỉ ra tập hợp S gồm tất cả các vecto khác \(\overrightarrow 0 \). Hãy chỉ ra tập hợp S gồm tất cả các vceto khác \(\overrightarrow 0 \), có điểm đầu và điểm cuối thuộc tập hợp {A; B; C; D; O}. Hãy chia tập S thành các nhóm sao cho hai vecto thuộc cùng một nhóm khi và chỉ khi chúng bằng nhau.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét các số có 9 chữ số khác nhau
Có 9 cách chọn chữ số ở vị trí đầu tiện. Có A 9 8 cách chọn 8 chữ số tiếp theo
Do đó có 9. A 9 8 số có 9 chữ số khác nhau
Gọi A là biến cố: “ số được chọn có đúng bốn chữ số lẻ sao cho số 0 luôn đứng giữa hai chữ số lẻ”
Có C 5 4 cách chọn 4 chữ số lẻ. Đầu tiên la xếp vị trí cho chữ số 0, do chữ số 0 không thể đứng đầu và cuối nên có 7 cách xếp.
Tiếp theo ta có A 4 2 cách chọn và xếp hai chữ số lẻ đứng 2 bên chữ số 0.
Khi đó có 6! Cách xếp 6 chữ số còn lại vào 6 vị trí còn lại.
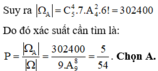

Câu 1 (3 điểm)
Viết tập hợp H bao gồm các số tự nhiên khác 0; nhỏ hơn 50 và chia hết cho 3.
\(H=\left\{3;6;9;12;15;18;21;24;27;30;33;36;39;42;45;48\right\}\)
Câu 2 (3 điểm)
Dùng các số tự nhiên 0; 2; 3; 4, hãy viết tất cả các số tự nhiên có 3 chữ số khác nhau:
- 203
- 204
- 230
- 234
- 240
- 243
- 302
- 304
- 320
- 324
- 340
- 342
- 402
- 403
- 420
- 423
- 430
- 432

2:
a: {1;4}; {1;5}; {1;7}; {1;9}; {3;4}; {3;5}; {3;7}; {3;9}; {8;4}; {8;5}; {8;7}; {8;9}
b: Số tập hợp thỏa mãn là;
\(3\cdot4=12\)

Chọn D
Không gian mẫu được mô tả là Ω : “Các số tự nhiên có 5 chữ số khác 0”.
Số phần tử của không gian mẫu là: ![]()
Gọi biến cố A: “Các số tự nhiên có 5 chữ số khác 0 trong đó chỉ có mặt ba chữ số khác nhau”.
Số cách chọn 3 chữ số phân biệt a, b, c từ 9 chữ số tự nhiên khác 0 là C 9 3 . Chọn 2 chữ số còn lại từ 3 chữ số đó, có 2 trường hợp sau:
TH1: Nếu cả 2 chữ số còn lại cùng bằng 1 trong 3 số a, b, c thì có 3 cách chọn. Mỗi hoán vị từ 5! hoán vị của 5 chữ số chẳng hạn a, a, a , b, c tạo ra một số tự nhiên; nhưng cứ hoán vị của các vị trí mà a, a, a chiếm chỗ thì chỉ tạo ra cùng 1 số tự nhiên. Do đó, trong TH1 có tất cả 3 . 5 ! 5 số tự nhiên.
TH2: 1 trong 2 chữ số còn lại bằng 1 trong 3 chữ số và chữ số kia bằng một chữ số a, b, c khác trong 3 chữ số đó thì có 3 cách chọn. Mỗi hoán vị từ 5! hoán vị chẳng hạn a, a, b, b, c tạo ra một số tự nhiên nhưng cứ 2! cách hoán vị a và 2! cách hoàn vị b mà vẫn cho ra cùng 1 số. Do đó, trong TH2 có tất cả: 3 . 5 ! 2 ! . 2 ! số tự nhiên.
Suy ra số phần tử của biến cố A là: ![]()
Vậy xác suất để trong số tự nhiên được lấy ra chỉ có mặt ba chữ số khác nhau là: 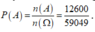

\(\overrightarrow{AO}=\overrightarrow{OC};\overrightarrow{DO}=\overrightarrow{OB}\);
\(\overrightarrow{OA}=\overrightarrow{CO};\overrightarrow{DO}=\overrightarrow{OB}\).

ABCD là hình vuông
\(\Rightarrow\Delta ABD\&\Delta ACD\) là tam vuông cân
\(\Rightarrow\left\{{}\begin{matrix}\left|\overrightarrow{AC}\right|=\left|\overrightarrow{AD}\right|.\sqrt[]{2}\\\left|\overrightarrow{BD}\right|=\left|\overrightarrow{AB}\right|.\sqrt[]{2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left|\overrightarrow{AC}\right|=\dfrac{\sqrt[]{2}}{2}.\sqrt[]{2}=1\\\left|\overrightarrow{BD}\right|=\dfrac{\sqrt[]{2}}{2}.\sqrt[]{2}=1\end{matrix}\right.\)
\(\left|\overrightarrow{OA}\right|=\left|\overrightarrow{AO}\right|=\dfrac{1}{2}.\left|\overrightarrow{AC}\right|\) (O là trung điểm AC)
\(\Rightarrow\left|\overrightarrow{OA}\right|=\left|\overrightarrow{AO}\right|=\dfrac{1}{2}.1=\dfrac{1}{2}\)



Tham khảo:
Tập hợp S là: \(S = \{ \overrightarrow {AB} ;\;\overrightarrow {AC} ;\;\overrightarrow {AD} ;\;\overrightarrow {AO} ;\;\overrightarrow {BA} ;\;\overrightarrow {BC} ;\;\overrightarrow {BD} ;\;\overrightarrow {BO} ;\;\overrightarrow {CB} ;\;\overrightarrow {CA} ;\;\overrightarrow {CD} ;\;\overrightarrow {CO} ;\;\overrightarrow {DB} ;\;\overrightarrow {DC} ;\;\overrightarrow {DA} ;\;\overrightarrow {DO} ;\;\overrightarrow {OB} ;\;\overrightarrow {OC} ;\;\overrightarrow {OD} ;\;\overrightarrow {OA} \} \)
Các nhóm trong S là:
\(\begin{array}{l}\{ \overrightarrow {AB} ;\overrightarrow {DC} \} ,\{ \overrightarrow {BA} ;\overrightarrow {CD} \} ,\{ \overrightarrow {AD} ;\overrightarrow {BC} \} ,\{ \overrightarrow {DA} ;\overrightarrow {CB} \} ,\\\{ \overrightarrow {AO} ;\overrightarrow {OC} \} ,\{ \overrightarrow {OA} ;\overrightarrow {CO} \} ,\{ \overrightarrow {OB} ;\overrightarrow {DO} \} ,\{ \overrightarrow {BO} ;\overrightarrow {OD} \} .\end{array}\)