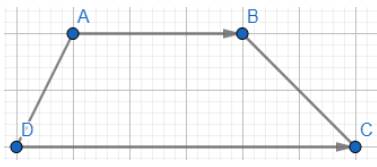
Cho hình thang cân ABCD với hai đáy AB, CD, \(AB < CD\). Hãy chỉ ra mối quan hệ về độ dài, phương, hướng giữa các cặp vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \), \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \), \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \). Có cặp vectơ nào trong các cặp vectơ trên bằng nhau hay không?



Dễ thấy:
\(AD = BC\) nhưng \(AD\) và \(BC\) không song song với nhau. Do đó hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \) không bằng nhau.
\(CD > AB\) do đó hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) không bằng nhau.
\(AC\) và \(BD\) không song song với nhau. Do đó hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \) không bằng nhau.