Trong tình huống mở đầu, gọi x và y lần lượt là số máy điều hoà loại hai chiều và một chiều mà cửa hàng cần nhập. Từ HĐ1, viết hệ bất phương trình hai ẩn x, y và chỉ ra một nghiệm của hệ này.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số tiền mua x chiếc điều hòa hai chiều là 20x (triệu đồng)
Số tiền mua y chiếc điều hòa một chiều là 10y (triệu đồng).
Số tiền khi mua x chiếc điều hòa hai chiều và y chiếc điều hòa một chiều là 20x+10y (triệu đồng).
a) Nhu cầu thị trường không quá 100 máy cả 2 loại có nghĩa là tổng số điều hòa nhập vào cũng không quá 100 máy: \(x + y \le 100\)
b)
1,2 tỉ đồng =1200 (triệu đồng)
Số vốn mua x điều hòa hai chiều và y chiếc điều hòa một chiều là 20x+10y (triệu đồng).
Do chủ cửa hàng có thể đầu tư không vượt quá 1,2 tỉ đồng nên ta có: \(20x + 10y \le 1200\)
\( \Leftrightarrow 2x + y \le 120\)
c)
Số tiền lãi khi bán x chiếc điều hòa hai chiều là 3,5x (triệu đồng)
Số tiền lãi khi bán y chiếc điều hòa một chiều là 2y (triệu đồng)
Tổng số tiền lãi là 3,5x+2y (triệu đồng)

a) Hai bất phương trình bài cho là bất phương trình bậc nhất hai ẩn.
b) (1; 1) là một nghiệm chung của hai BPT (1) và (2) vì:
Thay x=1;y=1 vào (1) ta được: 1-1<3 (Luôn đúng)
Thay x=1; y=1 vào (2) ta được: 1+2.1>-2 (Luôn đúng)

Gọi x và y lần lượt là số máy điều hoà loại hai chiều và một chiều mà cửa hàng cần nhập. \(x, y \in \mathbb N\)
Do nhu cầu thị trường không quá 100 máy cả 2 loại nên \(x + y \le 100\)
Do chủ cửa hàng có thể đầu tư không vượt quá 1,2 tỉ đồng nên: \(20x + 10y \le 1200\)
Tổng số tiền lãi là T = 3,5x+2y (triệu đồng).
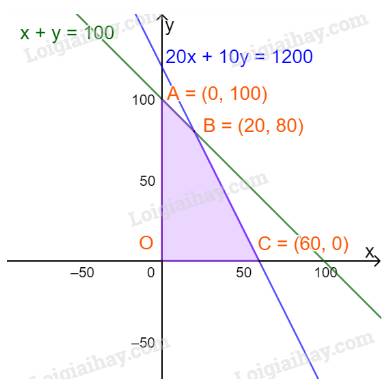
Các cặp (x;y) thỏa mãn thuộc miền tứ giác OABC, với A(0; 100), B(20; 80), C(60;0).
+) x = 0, y = 100 thì tiền lãi là 3,5.0+2.100=200 triệu đồng
+) x = 60, y = 0 thì tiền lãi là 3,5.60+2.0=210 triệu đồng
+) x = 20, y = 80 thì tiền lãi là 3,5.20+2.80=230 triệu đồng
Vậy cửa hàng cần nhập 20 máy điều hoà loại hai chiều và 80 máy một chiều thì lợi nhuận thu được là lớn nhất.

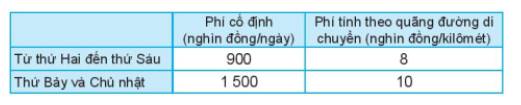
a) Số tiền ông An phải trả cho việc thuê xe ô tô từ thứ Hai đến thứ Sáu là:
900.5 + 8x = 4 500 + 8x (nghìn đồng).
Số tiền ông An phải trả cho việc thuê xe ô tô từ thứ Hai đến thứ Sáu là:
1 500.2 + 10y = 3 000 + 10y (nghìn đồng).
Tổng số tiền ông An phải trả cho việc thuê xe trong một tuần là:
4 500 + 8x + 3 000 + 10y = 7 500 + 8x + 10y (nghìn đồng).
Để tổng số tiền ông An phải trả không quá 14 triệu đồng thì
7 500 + 8x + 10y ≤ 14 000
⇔ 8x + 10y ≤ 6 500.
⇔ 4x + 5y ≤ 3 250.
Vậy bất phương trình biểu thị mối liên hệ giữa x và y sao cho tổng số tiền ông An phải trả không quá 14 triệu đồng là 4x + 5y ≤ 3 250.
b)
Vẽ đường thẳng d: 4x + 5y = 3 250 trên mặt phẳng tọa độ.
Lấy gốc tọa độ O(0; 0) và tính 4.0 + 5.0 = 0 < 3 250.
Do đó miền nghiệm của bất phương trình là nửa mặt phẳng có bờ là đường thẳng d không chứa gốc tọa độ và cả đường thẳng d (miền không bị gạch kể cả biên)
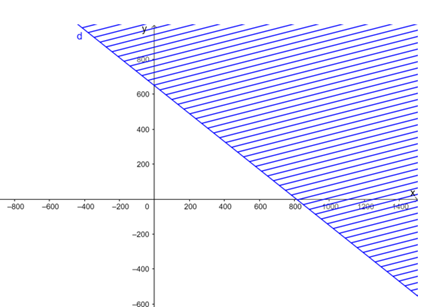
Tham khảo:
a)
Ta có 14 triệu = 14 000 (nghìn đồng)
Phí cố định là: 900.5 + 1500.2 = 7500 (nghìn đồng)
Phí tính theo quãng đường là:
x km trong các ngày từ thứ Hai đến thứ Sáu là 8x (nghìn đồng)
y km trong 2 cuối tuần là 10y (nghìn đồng)
Tổng số tiền ông An phải trả là 8x+10y +7500 (nghìn đồng)
Vì số tiền không quá 14 triệu đồng nên ta có :
\(\begin{array}{l}8x + 10y +7500 \le 14000\\ \Leftrightarrow 4x + 5y \le 3250\end{array}\)
Vậy bất phương trình cần tìm là \(4x + 5y \le 3250\)
b)
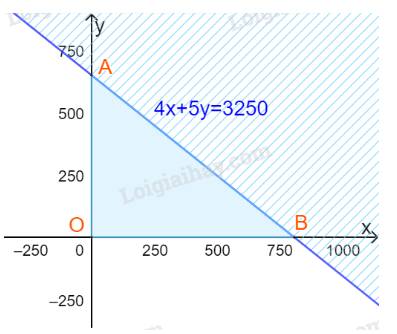
Bước 1: Vẽ đường thẳng \(4x + 5y = 3250\)(nét liền)
Bước 2: Thay tọa độ điểm O(0;0) vào biểu thức 4x+5y ta được:
4.0+5.0=0<3250
=> Điểm O thuộc miền nghiệm
=> Miền nghiệm là nửa mặt phẳng bờ là đường thẳng \(4x + 5y = 3250\) và chứa gốc tọa độ và (x;y) nằm trong miền tam giác OAB kể cả đoạn AB.

Bước 1:
Từ HĐ 1 ta có hai bất phương trình:
\(x + 2y \ge 400\left( 1 \right)\) và \(x + 2y < 400\left( 2 \right)\)
Thay x=100 và y=100 vào bất phương trình (1) ta được:
\(100 + 2.100 \ge 400 \Leftrightarrow 300 \ge 400\) (Vô lí)
=> Cặp số (x;y)=(100;100) không thỏa mãn bất phương trình (1).
Thay x=100 và y=100 vào bất phương trình (2) ta được:
\(100 + 2.100 < 400 \Leftrightarrow 300 < 400\) (Đúng)
=> Cặp số (x;y)=(100;100) thỏa mãn bất phương trình (2).
Cặp số (x;y)=(100;100) thỏa mãn bất phương trình (2) có nghĩa là nếu bán được 100 vé loại 1 và 100 vé loại 2 thì rạp chiếu phim phải bù lỗ.
Bước 2:
Thay x=150 và y=150 vào bất phương trình (1) ta được:
\(150 + 2.150 \ge 400 \Leftrightarrow 450 \ge 400\) (Đúng)
=> Cặp số (x;y)=(150;150) thỏa mãn bất phương trình (1).
Thay x=150 và y=150 vào bất phương trình (2) ta được:
\(150 + 2.150 < 400 \Leftrightarrow 450 < 400\) (Vô lí)
=> Cặp số (x;y)=(150;150) không thỏa mãn bất phương trình (2).
Cặp số (x;y)=(150;150) thỏa mãn bất phương trình (1) có nghĩa là nếu bán được 150 vé loại 1 và 150 vé loại 2 thì rạp chiếu phim không phải bù lỗ.
Chú ý
Khi thay cặp số (x;y)=(100;100) vào các bất phương trình bài cho đồng nghĩa với rạp chiếu phim bán được 100 vé loại 1 và 100 vé loại 2.

a) \(5x + 3y < 20\)
Đây là bất phương trình bậc nhất hai ẩn.
Chọn \(x = 0;y = 0\)
Khi đó bất phương trình tương đương với 5.0+3.0
Vậy (0;0) là một nghiệm của bất phương trình trên.
b) \(3x - \frac{5}{y} > 2\)
Đây không là bất phương trình bậc nhất hai ẩn vì có ẩn y ở mẫu.

Hướng dẫn giải
Anh có thể làm việc không nhiều hơn 22 giờ một tuần : x + y ≤ 22
Anh muốn kiếm tối thiểu 1.900.000 đồng một tuần : 100.000x + 80.000y ≥ 1.900.000.
Chọn A.

Chọn đáp án D
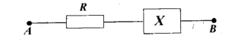
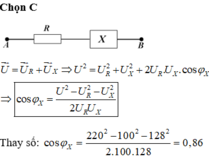
U → = U R → + U X → ⇒ U 2 = U R 2 + U X 2 + 2 U R . U X cos φ X ⇒ cos φ X = U 2 − U R 2 − U X 2 2 U R U X
Thay số: cos φ X = 220 2 − 100 2 − 128 2 2.100.128 = 0 , 86
- Lập hệ:
Do số lượng máy nhập vào phải là số tự nhiên nên ta có \(x \ge 0,y \ge 0\).
Từ HĐ 1 ta có hai bất phương trình là \(x + y \le 100\) và \(2x + y \le 120\)
Vậy hệ bất phương trình từ HĐ 1 là
\(\left\{ \begin{array}{l}x + y \le 100\\2x + y \le 120\\x \ge 0\\y \ge 0\end{array} \right.\).
Cặp số (x;y)=(50;10) là một nghiệm của hệ BPT vì thay x= 50, y= 10 ta được:
\(\left\{ {\begin{array}{*{20}{l}}
{50 + 10 \le 100}\, \text {(Đúng)}\\
{2.50 + 10 \le 120}\, \text {(Đúng)}\\
{50 \ge 0}\, \text {(Đúng)}\\
{10 \ge 0}\, \text {(Đúng)}
\end{array}} \right.\)