Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Lập hệ:
Do số lượng máy nhập vào phải là số tự nhiên nên ta có \(x \ge 0,y \ge 0\).
Từ HĐ 1 ta có hai bất phương trình là \(x + y \le 100\) và \(2x + y \le 120\)
Vậy hệ bất phương trình từ HĐ 1 là
\(\left\{ \begin{array}{l}x + y \le 100\\2x + y \le 120\\x \ge 0\\y \ge 0\end{array} \right.\).
Cặp số (x;y)=(50;10) là một nghiệm của hệ BPT vì thay x= 50, y= 10 ta được:
\(\left\{ {\begin{array}{*{20}{l}}
{50 + 10 \le 100}\, \text {(Đúng)}\\
{2.50 + 10 \le 120}\, \text {(Đúng)}\\
{50 \ge 0}\, \text {(Đúng)}\\
{10 \ge 0}\, \text {(Đúng)}
\end{array}} \right.\)

Gọi x và y lần lượt là số máy điều hoà loại hai chiều và một chiều mà cửa hàng cần nhập. \(x, y \in \mathbb N\)
Do nhu cầu thị trường không quá 100 máy cả 2 loại nên \(x + y \le 100\)
Do chủ cửa hàng có thể đầu tư không vượt quá 1,2 tỉ đồng nên: \(20x + 10y \le 1200\)
Tổng số tiền lãi là T = 3,5x+2y (triệu đồng).
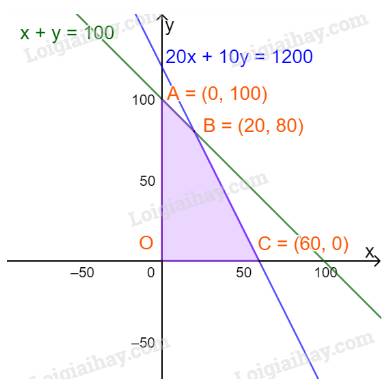
Các cặp (x;y) thỏa mãn thuộc miền tứ giác OABC, với A(0; 100), B(20; 80), C(60;0).
+) x = 0, y = 100 thì tiền lãi là 3,5.0+2.100=200 triệu đồng
+) x = 60, y = 0 thì tiền lãi là 3,5.60+2.0=210 triệu đồng
+) x = 20, y = 80 thì tiền lãi là 3,5.20+2.80=230 triệu đồng
Vậy cửa hàng cần nhập 20 máy điều hoà loại hai chiều và 80 máy một chiều thì lợi nhuận thu được là lớn nhất.

Bước 1:
Số tiền bán x vé loại 1 là: \(x.50\) (nghìn đồng)
Số tiền bán y vé loại 2 là: \(y.100\) (nghìn đồng)
Bước 2:
Số tiền thu được là
\(50x + 100y\) (nghìn đồng)
a)
Ta có 20 triệu = 20 000 (nghìn đồng)
Số tiền thu được khi bán x vé loại 1 và y vé loại 2 là \(50x + 100y\) (nghìn đồng)
Nên để số tiền thu được tối thiểu 20 triệu thì ta cần:
\(\begin{array}{l}50x + 100y \ge {20 000}\\ \Leftrightarrow x + 2y \ge 400\end{array}\)
Vậy các số nguyên không âm x và y phải thỏa mãn điều kiện \(x + 2y \ge 400\)
b)
Số tiền thu được khi bán x vé loại 1 và y vé loại 2 là \(50x + 100y\) (nghìn đồng)
Số tiền thu được nhỏ hơn 20 triệu thì:
\(\begin{array}{l}50x + 100y < {20 000}\\ \Leftrightarrow x + 2y < 400\end{array}\)
Chú ý:
- Số tiền tối thiểu thì ta phải lập bất phương trình với dấu “\( \ge \)”.
- Cần đổi 20 triệu đồng thành 20 000 nghìn đồng tránh lập sai bất phương trình.

Tham khảo:
a)
Bước 1: Ta có:
| Loại A | Loại B |
Giá mua vào | 10 triệu đồng/1 máy | 20 triệu đồng/1 máy |
Lợi nhuận | 2,5 triệu đồng/1 máy | 4 triệu đồng/1 máy |
Bước 2: Lập hệ bất phương trình
Vì số lượng máy là số tự nhiên nên ta có \(x \ge 0;y \ge 0\)
Vốn nhập vào x máy loại A và y máy loại B là \(10x + 20y\)(triệu đồng)
4 tỉ đồng=4000 (triệu đồng)
Vì số vốn ban đầu không vượt quá 4 tỉ đồng nên ta có bất phương trình
\(10x + 20y \le 4000\) \( \Leftrightarrow x + 2y \le 400\)
Vì tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy nên ta có \(x + y \le 250\).
Vậy ta có hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + 2y \le 400\\x + y \le 250\end{array} \right.\)
Bước 3: Xác định miền nghiệm
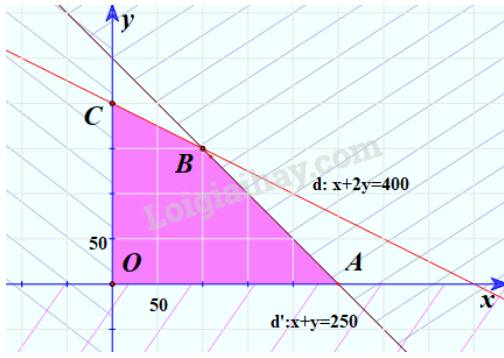
Miền nghiệm là tứ giác OABC với tọa độ các đỉnh này là O(0;0), A(250;0), B(100;150), C(0;200)
b) Lợi nhuận hàng tháng là F(x;y)=2,5x+4y(triệu đồng)
c) Ta cần tìm giá trị lớn nhất của F(x;y) khi (x;y) thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + 2y \le 400\\x + y \le 250\end{array} \right.\)
Ta có F(0;0)=0, F(250;0)=2,5.250+4.0=625
F(100;150)=2,5.100+4.150=850
F(0;200)=2,5.0+4.200=800
Giá trị lớn nhất là F(100;150)=850.
Vậy cửa hàng cần đầu tư kinh doanh 100 máy A và 150 máy B.
a) Số máy tính loại A cửa hàng cần nhập trong một tháng là x (máy), số máy tính loại B cửa hàng cần nhập trong một tháng là y (máy) (x,y≥0).
Do tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy: x + y ≤ 250
Tổng số vốn cửa hàng cần nhập hai loại A và B: 10x + 20y (triệu đồng)
Vì mỗi chiếc máy tính loại A có giá 10 triệu và mỗi máy tính loại B có giá 20 triệu nên tổng số vốn cửa hàng cần nhập hai loại A và B: 10x + 20y (triệu đồng)
Vì số vốn ban đầu không vượt quá 4 tỉ đồng nên ta có: 10x + 20y ≤ 4 000 hay x + 2y ≤ 400.
Ta có hệ bất phương trình: \(\left\{{}\begin{matrix}x\ge0\\y\ge0\\x+y\le250\\x+2y\le400\end{matrix}\right.\)
Ta xác định miền nghiệm của hệ bất phương trình trên:
+) Miền nghiệm D1 của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy chứa điểm (1;0).
+) Miền nghiệm D2 của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox chứa điểm (0;1).
+) Xác định miền nghiệm D3 của bất phương trình x + y ≤ 250.
- Vẽ đường thẳng d: x + y = 250.
- Vì 0 + 0 = 0 < 250 nên tọa độ điểm O(0;0) thỏa mãn bất phương trình x + y ≤ 250
Do đó miền nghiệm D3 của bất phương trình x + y ≤ 250 là nửa mặt phẳng bờ d chứa gốc tọa độ.
+) Xác định miền nghiệm D4 của bất phương trình x + 2y ≤ 400.
- Vẽ đường thẳng d’: x + 2y = 400.
- Vì 0 + 2.0 = 0 < 400 nên tọa độ điểm O(0;0) thỏa mãn bất phương trình x + 2y < 400
Do đó miền nghiệm D4 của bất phương trình x + 2y < 400 là nửa mặt phẳng bờ d’ chứa gốc tọa độ.
Miền nghiệm của hệ bất phương trình trên là tứ giác OABC với O(0;0), A(0; 200), C(100;150), B(250;0)
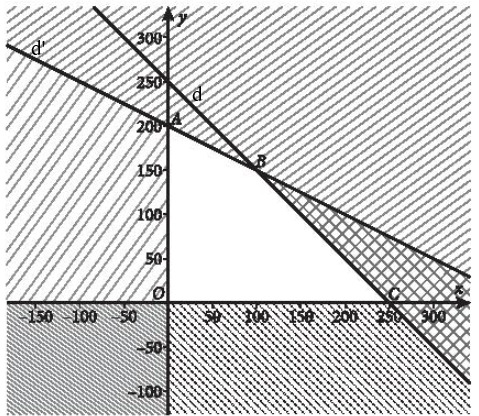
b) Lợi nhuận mà cửa hàng thu được trong tháng đó khi bán x máy tính loại A và y máy tính loại B là: F(x;y) = 2,5x + 4y (triệu đồng).
Vậy F(x;y) = 2,5x + 4y.
c) Bài toán chuyển về tìm giá trị lớn nhất của F(x;y) với (x;y) thuộc miền nghiệm của hệ bất phương trình \(\left\{{}\begin{matrix}x\ge0\\y\ge0\\x+y\le250\\x+2y\le400\end{matrix}\right.\)
Người ta đã chứng minh được, giá trị F(x; y) lớn nhất tại (x; y) là tọa độ của một trong bốn đỉnh O; A; B; C.
Tại O(0; 0), ta có: F(0; 0) = 2,5 . 0 + 4 . 0 = 0;
Tại A(0; 200), ta có: F(0; 200) = 2,5 . 0 + 4 . 200 = 800;
Tại B(100; 150), ta có: F(100; 150) = 2,5 . 100 + 4 . 150 = 850;
Tại B(250; 0), ta có: F(250; 0) = 2,5 . 250 + 4 . 0 = 625.
Do đó F(x;y) lớn nhất bằng 850 tại x = 100 và y = 150.
Vậy cửa hàng cần nhập 100 máy loại A, 150 máy loại B để cửa hàng thu được lợi nhuận lớn nhất là 850 triệu đồng.

Đổi 60g=0,06kg, 50g=0,05kg
Lượng đường cần cho x chiếc bánh nướng là 0,06x kg
Lượng đường cần cho y chiếc bánh dẻo là 0,05y kg
Vì lượng đường đã nhập về là 500kg và lượng đường sản xuất bánh không vượt quá lượng đường đã nhập về nên ta có:
\(0,06x + 0,05y \le 500\)

Dễ thấy: Hoa hồng nhung là loại hoa bán được nhiều nhất trong dịp năm nay, do đó cửa hàng nên nhập loại hoa này nhiều nhất để bán vào dịp 14 tháng 2 năm sau.

TRẢ LỜI:
Gọi x, y, z lần lượt là số đồng tiền xu loại 2000 đồng, 1000 dồng, 500 đồng.
Điều kiện là x, y, z nguyên dương
Ta có hệ phương trình
x + y + z = 1450 (1)
4x + 2y + z = 3000 (2)
2x + y - 2z = 0 (3)
Trừ từng vế tương ứng của phương trình (2) với phương trình (1) ta được
3x + y = 1550
Cộng từng vế tương ứng của các phương trình (1), (2) và (3) ta có :
7x + 4y = 4450.
Giải hệ gồm hai phương trình (4) và (5) ta được.
x = 350, y = 500.
Thay các giá trị của x, y vào phương trình (1) ta được z = 600.
Vậy cửa hàng đổi được 350 đồng tiền xu loại 2000 đồng, 500 đồng tiền loại 1000 đồng và 600 đồng tiền xu loại 500 đồng.
Số tiền mua x chiếc điều hòa hai chiều là 20x (triệu đồng)
Số tiền mua y chiếc điều hòa một chiều là 10y (triệu đồng).
Số tiền khi mua x chiếc điều hòa hai chiều và y chiếc điều hòa một chiều là 20x+10y (triệu đồng).
a) Nhu cầu thị trường không quá 100 máy cả 2 loại có nghĩa là tổng số điều hòa nhập vào cũng không quá 100 máy: \(x + y \le 100\)
b)
1,2 tỉ đồng =1200 (triệu đồng)
Số vốn mua x điều hòa hai chiều và y chiếc điều hòa một chiều là 20x+10y (triệu đồng).
Do chủ cửa hàng có thể đầu tư không vượt quá 1,2 tỉ đồng nên ta có: \(20x + 10y \le 1200\)
\( \Leftrightarrow 2x + y \le 120\)
c)
Số tiền lãi khi bán x chiếc điều hòa hai chiều là 3,5x (triệu đồng)
Số tiền lãi khi bán y chiếc điều hòa một chiều là 2y (triệu đồng)
Tổng số tiền lãi là 3,5x+2y (triệu đồng)