Vẽ hình biểu diễn của hình chóp S.ABCD có đáy ABCD là hình thang, AB song song với CD và AB = 2cm, CD = 6cm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 8 2023
Gọi O là giao của AC với BD trong mp(ABCD)
Trong mp(SBD), gọi E là giao của SO với DM
\(E\in SO\subset\left(SAC\right)\)
\(E\in DM\subset\left(ADM\right)\)
=>E thuộc (SAC) giao (ADM)
mà \(A\in\left(SAC\right)\cap\left(ADM\right)\)
nên \(\left(SAC\right)\cap\left(ADM\right)=EA\)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
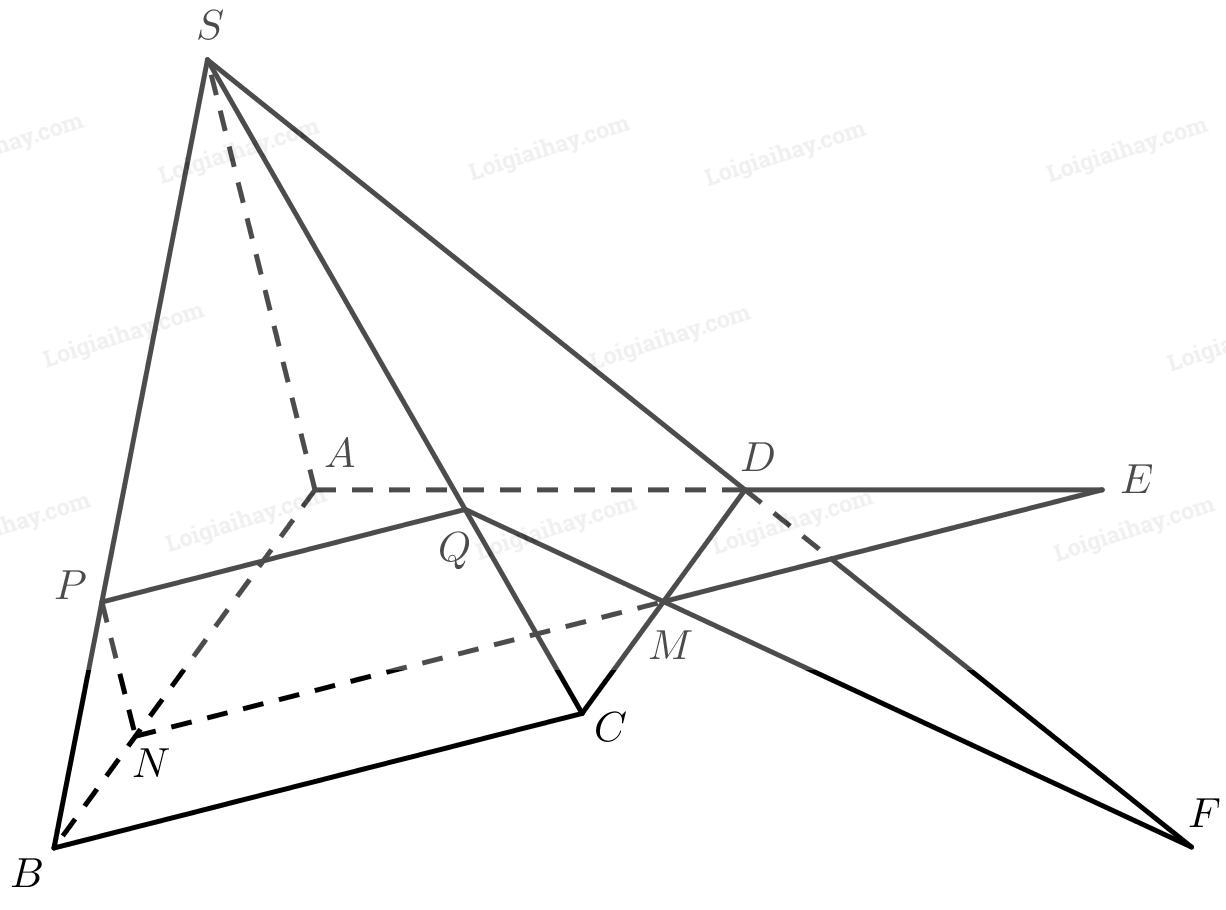
Qua \(M\) dựng đường thẳng song song với \(BC\), cắt \(AB\) tại \(N\).
Qua \(N\) dựng đường thẳng song song với \(SA\), cắt \(SB\) tại \(P\).
Qua \(P\) dựng đường thẳng song song với \(BC\), cắt \(SC\) tại \(Q\).
Vì \(MN\parallel BC,NP\parallel SA\) nên \(\left( {MNPQ} \right) \equiv \left( P \right)\).
Ta có:
\(\begin{array}{l}MN = \left( P \right) \cap \left( {ABC{\rm{D}}} \right)\\NP = \left( P \right) \cap \left( {SAB} \right)\\PQ = \left( P \right) \cap \left( {SBC} \right)\\MQ = \left( P \right) \cap \left( {SC{\rm{D}}} \right)\end{array}\)
Gọi \(E\) là giao điểm của \(A{\rm{D}}\) và \(MN\), \(F\) là giao điểm của \(S{\rm{D}}\) và \(MQ\). Ta có:
\(\begin{array}{l}\left. \begin{array}{l}E \in A{\rm{D}} \subset \left( {SA{\rm{D}}} \right)\\E \in MN \subset \left( P \right)\end{array} \right\} \Rightarrow E \in \left( P \right) \cap \left( {SA{\rm{D}}} \right)\\\left. \begin{array}{l}F \in S{\rm{D}} \subset \left( {SA{\rm{D}}} \right)\\F \in MQ \subset \left( P \right)\end{array} \right\} \Rightarrow F \in \left( P \right) \cap \left( {SA{\rm{D}}} \right)\\ \Rightarrow EF = \left( P \right) \cap \left( {SA{\rm{D}}} \right)\end{array}\)
22 tháng 10 2016
Tớ biết làm nè
.
.
.
.
.
.
.
.
.
.
.
Biết làm cl í, tin người vcl:))
QT
Quoc Tran Anh Le
Giáo viên
23 tháng 8 2023
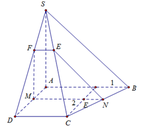
Ta có: SD và AB chéo nhau.
Vì AB và SD chéo nhau nên AB không nằm trong mp(SCD).
Vì AB // CD nên AB // mp(SCD).
Vậy (SCD) là mặt phẳng chứa SD và song song với AB.
QT
Quoc Tran Anh Le
Giáo viên
23 tháng 8 2023
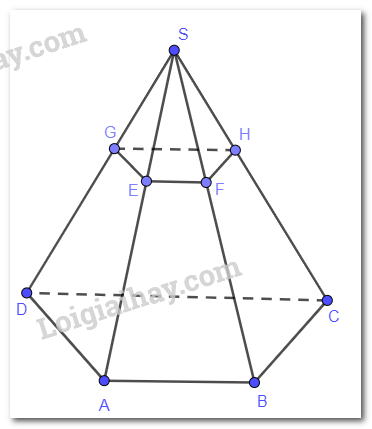
Mặt phẳng (SAD) chứa đường thẳng AD song song với mp(P) nên mặt phẳng (P) cắt (SAD) theo giao tuyến song song với AD. Vẽ EG // AD (G thuộc SD) thì EG là giao tuyến của (P) và (SAD).
Mặt phẳng (SAB) chứa đường thẳng AB song song với mp(P) nên mặt phẳng (P) cắt (SAB) theo giao tuyến song song với AB. Vẽ EF // AB (F thuộc SB) thì EF là giao tuyến của (P) và (SAB).
Ta có AB // CD, EF // AB suy ra CD // EF hay CD // mp(P)
Mặt phẳng (SCD) chứa đường thẳng CD song song với mp(P) nên mặt phẳng (P) cắt (SCD) theo giao tuyến song song với CD. Vẽ GH // CD (H thuộc SC) thì GH là giao tuyến của (P) và (SCD).
FH thuộc (P), FH thuộc (SBC) suy ra FH là giao tuyến của (P) và (SBC).
Tứ giác EFGH có EF // GH (vì cùng song song với CD) suy ra EFGH là hình thang.
Tham khảo:
Hình chóp S.ABCD có các mặt bên là hình tam giác nên hình biểu diễn của nó cũng các mặt bên là hình tam giác
Hình thang ABCD có AB//CD và AB=2cm, CD=6cm nên hình biểu diễn của ABCD là một hình thang có đáy CD gấp ba đáy BC
Từ đó, ta vẽ được hình biểu diễn của S.ABCD.