Cho góc lượng giác có số đo bằng \(\frac{{5\pi }}{6}\)
a) Xác định điểm M trên đường tròn lượng giác biểu diễn góc lượng giác đã cho.
b) Tính các giá trị lượng giác của góc lượng giác đã cho.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
Quoc Tran Anh Le
Giáo viên
21 tháng 9 2023
a) Ta thấy \(\sin t = {y_M}\) là tung độ của điểm M trên đường tròn lượng giác và c\(\cos t = {x_M}\) là hoành độ của điểm M trên đường tròn lượng giác.
Với mỗi điểm M xác định, ta chỉ có 1 tung độ và hoành độ duy nhất
Nên ta chỉ xác định duy nhất giá trị sint và cost.
b,
Nếu \(t \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\), ta có: \(\tan t = \frac{{\sin t}}{{{\rm{cost}}}} = \frac{{{y_M}}}{{{x_M}}}\)( \({x_M} \ne 0\))
Nếu \(t \ne k\pi ,k \in \mathbb{Z}\), ta có: \(\cot t = \frac{{{\rm{cost}}}}{{{\rm{sint}}}} = \frac{{{x_M}}}{{{y_M}}}\)( \({y_M} \ne 0\))
Do \({x_M}\), \({y_M}\)xác định duy nhất nên \(\tan t\), \(\cot t\)xác định duy nhất.
21 tháng 9 2023
Tham khảo:
Điểm biểu diễn góc lượng giác có số đo bằng \( - \frac{{15\pi }}{4} = - \frac{{7\pi }}{4} + ( - 1).2\pi \) được xác định là điểm M.
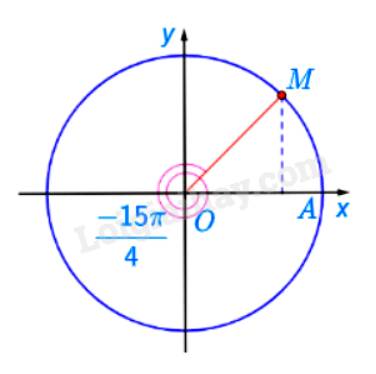
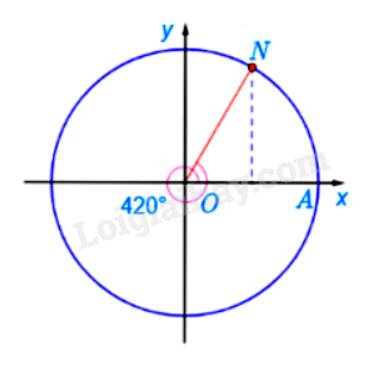
Ta có \(\frac{{420}}{{360}} = 1+ \frac{1}{6}\) Ta chia đường tròn thành 6 phần bằng nhau. Khi đó điểm N là điểm biểu diễn bởi góc có số đo \({420^ \circ }\)
21 tháng 9 2023
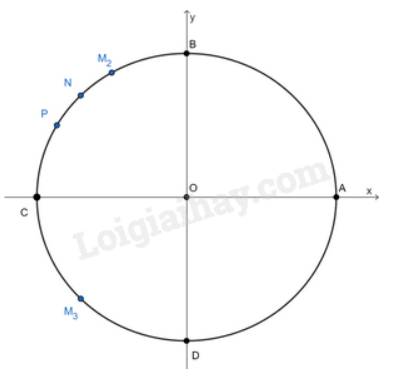
a) Ta có: \(\frac{{\frac{{2\pi }}{3}}}{{2\pi }} = \frac{1}{3}\). Ta chia đường tròn thành 3 phần bằng nhau. Khi đó điểm \({M_2}\) là điểm biểu diễn bởi góc có số đo \(\frac{{2\pi }}{3}\).
b) Ta có \( - \frac{{11\pi }}{4} = - \frac{{3\pi }}{4} + \left( { - 1} \right).2\pi \). Do đó điểm biểu diễn bởi góc \( - \frac{{11\pi }}{4}\) trùng với góc \( - \frac{{3\pi }}{4}\) và là điểm \({M_3}\).
c) Ta có \(\frac{{150}}{{180}} = \frac{5}{6}\). Ta chia nửa đường tròn thành 6 phần bằng nhau. Khi đó P là điểm biểu diễn bởi góc \({150^0}\)
d) Ta có \( - {225^0} = - {180^0} - {45^0}\). Do đó điểm biểu diễn N là điểm biểu diễn bởi góc \( - {225^0}\)
HQ
Hà Quang Minh
Giáo viên
25 tháng 8 2023
a, Với mọi \(x\in R\), ta có: \(-1\le sin\left(x\right)\le1\)
Do đó, không có giá trị nào của x để \(sin\left(x\right)=1,5\)
b, Những điểm biểu diễn góc lượng giác có \(sin\left(x\right)=0,5\) là M và N.
Điểm M biểu diễn cho các góc lượng giác có số đo là \(\dfrac{\pi}{6}+k2\pi,k\in Z\)
Điểm N biểu diễn cho các góc lượng giác có số đo là \(\dfrac{5\pi}{6}+k2\pi,k\in Z\)
QT
Quoc Tran Anh Le
Giáo viên
21 tháng 9 2023
Điểm biểu diễn góc lượng giác x có \(cosx = \frac{{ - 1}}{2}\) là M và N.
Số đo góc lượng giác có điểm biểu diễn M là: \(\frac{{2\pi }}{3} + k2\pi ,k \in \mathbb{Z}\).
Số đo góc lượng giác có điểm biểu diễn N là: \(\frac{{4\pi }}{3} + k2\pi ,k \in \mathbb{Z}\).
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Ta có: \(\frac{{25\pi }}{3} = \frac{\pi }{3} + 4.2\pi .\) Do đó điểm biểu diễn cung lượng giác \(\frac{{25\pi }}{3}\) trùng với điểm biểu diễn cung lượng giác \(\frac{\pi }{3}\).
Vậy ta chọn đáp án A
QT
Quoc Tran Anh Le
Giáo viên
21 tháng 9 2023
a) Ta có \( - {1485^ \circ } = - {45^ \circ } + ( - 4){.360^ \circ }\). Vậy điểm biểu diễn góc lượng giác có số đo \( - {1485^ \circ }\)là điểm M trên đường tròn lượng giác thuộc góc phần tư thứ IV sao cho \(\widehat {AMO} = {45^ \circ }\)
b) Ta có \(\frac{{19\pi }}{4} = \frac{{3\pi }}{4} + 4\pi \). Vậy điểm biểu diễn góc lượng giác có số đo \(\frac{{19\pi }}{4}\) là điểm N trên phần đường tròn lượng giác thuộc góc phần tư thứ II sao cho \(\widehat {AMO} = \frac{{3\pi }}{4}\).
Tham khảo:
a) Ta chia nửa đường tròn thành 6 phần bằng nhau. Khi đó điểm M là điểm biểu diễn bởi góc có số đo \(\frac{{5\pi }}{6}\)
b) Ta có:
\(\sin \left( {\frac{{5\pi }}{6}} \right) = \frac{1}{2};\cos \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - \sqrt 3 }}{2};\tan \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - \sqrt 3 }}{3};\cot \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - 3}}{{\sqrt 3 }}\)