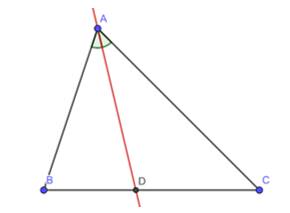
Vẽ và cắt hình tam giác ABC rồi gấp hình sao cho cạnh AB trùng với cạnh AC ta được nếp gấp AD (Hình 1). Đoạn thẳng AD nằm trên tia phân giác của góc nào của tam giác ABC?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: góc AB’M là góc ngoài của tam giác MB’C
Nên ∠(BMC) + ∠C= (AB'M) ⇒ ∠(AB'M) > ∠C

Bài 1:
Xét ΔADO vuông tại D và ΔAEO vuông tại E có
AO chung
\(\widehat{DAO}=\widehat{EAO}\)
Do đó: ΔADO=ΔAEO
Suy ra: OD=OE
Bài 2:
a: Xét ΔABE và ΔACD có
AB=AC
\(\widehat{BAE}\) chung
AE=AD
Do đó: ΔABE=ΔACD
Suy ra: BE=CD
b: Xét ΔBDC và ΔCEB có
BD=EC
\(\widehat{DBC}=\widehat{ECB}\)
BC chung
DO đó: ΔBDC=ΔCEB
Suy ra: \(\widehat{ODB}=\widehat{OEC}\)
Xét ΔODB và ΔOEC có
\(\widehat{ODB}=\widehat{OEC}\)
BD=CE
\(\widehat{DBO}=\widehat{ECO}\)
Do đó: ΔODB=ΔOEC

a. DAC=60 bVÌ Ax là tia phân giác của DAC nên DAx=CAx=30 độ.Mà BAD=30 độ(gt)->ad là tia phân giác của DAC
c. BAD,DAE,EAC,BAE,BAC,DEC
AD nằm trên tia phân giác của góc A