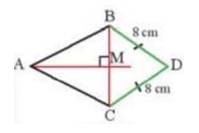
Quan sát Hình 12, cho biết AM là đường trung trực của đoạn thẳng BC và DB = DC = 8 cm. Chứng minh rằng ba điểm A, M, D thẳng hàng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 4 2023
a: ΔABC cân tại A
mà AM là đường cao
nên AM là trung trực của BC(1)
b: DB=DC
nên D nằm trên trung trực của BC(2)
(1), (2) =>A,M,D thẳng hàng
12 tháng 9 2019
a) Xét ∆ABC có : .
AM là trung tuyến
=> ∆ABC cân tại A , trung tuyến AM vừa là trung trực vừa là phân giác
b) Vì AM là trung trực ∆ABC
=> AMC = 90°
Xét ∆BDC có :
DM là trung tuyến
=> ∆BDC cân tại D , trung tuyến DM là trung trực và là phân giác
=> DMC = 90°
Ta có :
AMD = AMC + DMC
AMD = 90° + 90° = 180°
=> AMD là góc bẹt
=> A, M , D thẳng hàng
TN
19 tháng 8 2018
a/ áp dụng định lý py - ta - go vào tam giác ABC vuông tại A có :
AB2 +AC2 = BC2
<=> 62 +AC2 = 102
<=> AC2 = 64
<=> AC=8 (cm )
ta có AB < AC < BC (6 < 8 < 10 )
=> \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\) ( quan hệ giữa góc và cạnh )
b/ xét tam giác CAB và CAD có
CA chung
AB = AD ( vì A là trung điểm của BD )
\(\widehat{CAB}=\widehat{CAD}\)( = 90 độ )
=> tam giác CAB = tam giác CAD ( c - g - c )
=> CB = CD
=> tam giác BCD cân tại C
các câu còn lại mk k biết làm dâu
học tốt
Xét tam giác BCD có BD = CD ( giả thiết )
\( \Rightarrow \) D thuộc trung trực BC do cách đều 2 đầu mút đoạn BC
Mà AM là trung trực của BC
\( \Rightarrow \) D thuộc đường thẳng AM
\( \Rightarrow \) A, M, D thẳng hàng