Quan sát Hình 10.
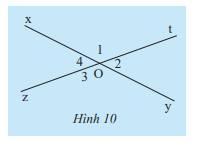
a) Hãy dùng thước đo góc để đo \(\widehat {{O_1}}\)và \(\widehat {{O_3}}\). So sánh số đo hai góc đó.
b) Hãy dùng thước đo góc để đo \(\widehat {{O_2}}\) và \(\widehat {{O_4}}\). So sánh số đo hai góc đó.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = (\widehat {{O_1}} + \widehat {{O_2}}) + \widehat {{O_3}}\)=\(\widehat {x'Oy} + \widehat {{O_3}}\), mà \(\widehat {x'Oy} + \widehat {{O_3}}\)= 180\(^\circ \) ( 2 góc kề bù)
Vậy \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = 180^\circ \)
b) Vì \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = 180^\circ \)
\(\begin{array}{l} \Rightarrow 60^\circ + \widehat {{O_2}} + 70^\circ = 180^\circ \\ \Rightarrow \widehat {{O_2}} = 180^\circ - 60^\circ - 70^\circ = 50^\circ \end{array}\)
Vậy \(\widehat {{O_2}} = 50^\circ \)

Sau khi đo, ta thấy bốn góc \(\widehat {\rm{A}}\), \(\widehat {\rm{B}}\), \(\widehat {\rm{C}}\), \(\widehat {\rm{D}}\) có số đo bằng nhau và bằng \(90^\circ \)

Sau khi đo góc ta thấy cặp góc \(\widehat {{A_1}}\) và \(\widehat {\rm{D}}\), \(\widehat {{{\rm{C}}_{\rm{1}}}}\) và \(\widehat {\rm{D}}\) bằng nhau
Mà các góc ở vị trí đồng vị
Suy ra: \(AB\) // \(CD\); \(AD\) // \(BC\)

a) Hai góc \(\widehat {xOy}\) và \(\widehat {yOz}\) có cạnh Oy chung, không có điểm trong chung
b) Ta có:
\(\begin{array}{l}\widehat {xOy} = 30^\circ ,\widehat {yOz} = 45^\circ ,\widehat {xOz} = 75^\circ \\ \Rightarrow \widehat {xOy} + \widehat {yOz} = \widehat {xOz}\end{array}\)
c) Ta có: \(\widehat {mOn} + \widehat {nOp} = 33^\circ + 147^\circ = 180^\circ \)

1) Các đỉnh: A, B, C, D
Các cạnh: AB, BC, CD, DA
Các đường chéo: AC, BD
2) Độ dài các cạnh của hình vuông đều bằng nhau
Độ dài 2 đường chéo của hình vuông bằng nhau
3) Các góc của hình vuông đều bằng nhau và bằng 90o

a.
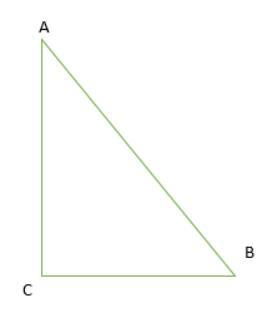
Góc CAB có số đo là 40 độ
Góc ABC có số đo là 50 độ
Góc ACB có số đo là 90 độ
b. Tổng ba góc trong tam giác là: 180 độ bằng với kết quả của các bạn khác.

1) Đỉnh: A, B, C, D
Cạnh: AB, BC, CD, DA
Đường chéo: AC, BD
Hai cạnh đối: AB và CD; BC và AD
2) Ta đo được: \(\widehat{A} = 90^0; \widehat{B} = 90^0; \widehat{C} = 90^0; \widehat{D} = 90^0\). Vậy các góc của hình chữ nhật đều bằng nhau và bằng 90o
3) Ta đo được: AB = CD ; AD = BC nên hai cạnh đối của hình chữ nhật bằng nhau
AC = BD nên hai đường chéo của hình chữ nhật bằng nhau.

a) Các góc kề với \(\widehat {tOz}\)là: \(\widehat {zOy},\widehat {zOn},\widehat {zOm}\)
b) Ta có: \(\widehat {mOn}\) = 30\(^\circ \) nên góc kề bù với \(\widehat {mOn}\) có số đo là: 180\(^\circ \) - 30\(^\circ \) = 150\(^\circ \)
c) Ta có:
\(\begin{array}{l}\widehat {mOn} + \widehat {nOy} + \widehat {yOt} = 180^\circ \\ \Rightarrow 30^\circ + \widehat {nOy} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {nOy} = 180^\circ - 30^\circ - 90^\circ = 60^\circ \end{array}\)
Vậy \(\widehat {nOy} = 60^\circ \)
d) Ta có: \(\widehat {tOz} = 45^\circ \) nên góc kề bù với \(\widehat {tOz}\) có số đo là: 180\(^\circ \) - 45\(^\circ \) = 135\(^\circ \)

Ta chia tứ giác ABCD thành tam giác ACD và tam giác ABC
\( \Rightarrow \) Số đo tổng các góc tam giác ACD = tổng số đo các góc tam giác ABC = \({180^o}\)
\( \Rightarrow \)Tổng số đo các góc trong tứ giác ABCD = tổng số đo các góc 2 tam giác ACD và ABC \( = {2.180^o} = {360^o}\)
Ta có:
\(\begin{array}{l}a)\widehat {{O_1}} = 135^\circ ;\widehat {{O_3}} = 135^\circ \Rightarrow \widehat {{O_1}} = \widehat {{O_3}}\\b)\widehat {{O_2}} = 45^\circ ;\widehat {{O_4}} = 45^\circ \Rightarrow \widehat {{O_2}} = \widehat {{O_4}}\end{array}\)