Cho hình thoi ABCD có góc ABC = 60 độ, cạnh bằng 4. Từ đỉnh A kẻ AM vuông góc với BC, AN vuông CD.
a) Chứng minh tam giác MAN đồng dạng với tam giác ABC
b) Chứng minh MN song song BD
c) Tính chu vi, diện tích hình thoi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 1 2019
tu ve hinh :
xet tamgiac AMN can tai A (gt) => goc AMN = goc ANM va AM = AN (dn)
AH vuong goc voi MN => goc AHN = goc AHM = 90o (dn)
=> tamgiac AMH = tamgiac ANH (ch - gn)
=> goc NAH = goc MAH (dn) ma AH nam giua AN va AM
=> AH la phan giac cua goc MAN
25 tháng 5 2022
a) △APQ và △BMQ có: \(\widehat{PAQ}=\widehat{MBQ}=45^0;\widehat{AQP}=\widehat{BQM}\).
\(\Rightarrow\)△APQ∼△BMQ (g-g)
\(\Rightarrow\dfrac{QP}{QM}=\dfrac{QA}{QB}\Rightarrow\dfrac{QP}{QA}=\dfrac{QM}{QB}\)
△ABQ và △PMQ có: \(\dfrac{QP}{QA}=\dfrac{QM}{QB};\widehat{AQB}=\widehat{PQM}\)
\(\Rightarrow\)△ABQ∼△PMQ (c-g-c).
25 tháng 5 2022
b) △ABQ∼△PMQ \(\Rightarrow\dfrac{PM}{AB}=\dfrac{PQ}{AQ};\widehat{BAQ}=\widehat{MPQ}\Rightarrow MP=\dfrac{PQ}{AQ}.AB\)
△APQ và △BPA có: \(\widehat{QAP}=\widehat{ABP}=45^0;\widehat{APB}\) là góc chung.
\(\Rightarrow\)△APQ∼△BPA (g-g)
\(\Rightarrow\widehat{AQP}=\widehat{BAP}\)
\(\widehat{APM}=\widehat{APQ}+\widehat{MPQ}=180^0-45^0-\widehat{AQP}+\widehat{BAQ}=180^0-45^0-\left(\widehat{BAP}-\widehat{BAQ}\right)=180^0-45^0-45^0=90^0\)
\(\Rightarrow\)MP⊥AN tại P.
△MPN và △AHN có: \(\widehat{MPN}=\widehat{AHN}=90^0;\widehat{ANM}\) là góc chung.
\(\Rightarrow\)△MPN∼△AHN (g-g)
\(\Rightarrow\dfrac{AH}{MP}=\dfrac{AN}{MN};\dfrac{NP}{NH}=\dfrac{NM}{NA}\Rightarrow\dfrac{NP}{NM}=\dfrac{NH}{NA}\)
△APQ và △AMN có: \(\dfrac{NP}{NM}=\dfrac{NH}{NA};\widehat{MAN}\) là góc chung.
\(\Rightarrow\)△APQ∼△AMN (c-g-c)
\(\Rightarrow\dfrac{AQ}{AN}=\dfrac{PQ}{MN}\Rightarrow\dfrac{MN}{AN}=\dfrac{PQ}{AQ}\)
\(\dfrac{AH}{MP}=\dfrac{AN}{MN}\Rightarrow AH=MP.\dfrac{AN}{MN}=\dfrac{PQ}{AQ}.AB.\dfrac{AN}{AM}=AB\) không đổi.
14 tháng 4 2023
a: Xét ΔAIB vuông tại I và ΔAEC vuông tại E có
góc A chung
=>ΔAIB đồng dạng với ΔAEC
=>AI/AE=AB/AC
=>AI/AB=AE/AC
b: Xét ΔAIE và ΔABC có
AI/AB=AE/AC
góc A chung
=>ΔAIE đồg dạng với ΔABC
YN
30 tháng 4 2022
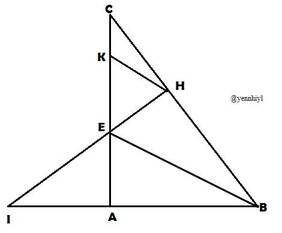
a) Xét \(\Delta ABE\) và \(\Delta HBE\):
BE chung
\(\widehat{ABE}=\widehat{EBH}\)
\(\widehat{EAB}=\widehat{EHB}=90^o\)
\(\Rightarrow\Delta ABE=\Delta HBE\left(ch-gn\right)\)
b) \(\widehat{EBH}=\dfrac{1}{2}\widehat{B}=30^o\)
\(\widehat{ACB}=90^o-\widehat{B}=30^o\)
\(\Rightarrow\Delta EBC\) cân tại E
Mà EH vuông góc BC
\(\Rightarrow HB=HC\)
c) \(\widehat{HEB}=90^o-\widehat{EBH}=60^o\)
\(KH//BE\Rightarrow\widehat{KHE}=\widehat{HEB}=60^o\)
\(\widehat{HEB}+\widehat{AEB}=60^o+60^o=120^o\)
\(\Rightarrow\widehat{KEH}=180^o-120^o=60^o\)
\(\Rightarrow\Delta EHK\) đều
d) Theo phần a. \(\Delta ABE=\Delta HBE\Rightarrow AE=EH\)
\(\Delta IAE\) vuông ở A \(\Rightarrow IE>AE\)
\(\Rightarrow IE>EH\)
1 tháng 5 2022
a) Xét ΔABEΔABE và ΔHBEΔHBE:
BE chung
ˆABE=ˆEBHABE^=EBH^
ˆEAB=ˆEHB=90oEAB^=EHB^=90o
⇒ΔABE=ΔHBE(ch−gn)⇒ΔABE=ΔHBE(ch−gn)
b) ˆEBH=12ˆB=30oEBH^=12B^=30o
ˆACB=90o−ˆB=30oACB^=90o−B^=30o
⇒ΔEBC⇒ΔEBC cân tại E
Mà EH vuông góc BC
⇒HB=HC⇒HB=HC
c) ˆHEB=90o−ˆEBH=60oHEB^=90o−EBH^=60o
KH//BE⇒ˆKHE=ˆHEB=60oKH//BE⇒KHE^=HEB^=60o
ˆHEB+ˆAEB=60o+60o=120oHEB^+AEB^=60o+60o=120o
⇒ˆKEH=180o−120o=60o⇒KEH^=180o−120o=60o
⇒ΔEHK⇒ΔEHK đều
d) Theo phần a. ΔABE=ΔHBE⇒AE=EHΔABE=ΔHBE⇒AE=EH
ΔIAEΔIAE vuông ở A ⇒IE>AE