Trong mỗi hình bên (H.4.39), hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
+)Xét hai tam giác vuông ABC và XYZ có:
\(\widehat A = \widehat X( = 90^\circ )\) (gt)
AC=XZ (gt)
\(\widehat C = \widehat Z\) (gt)
\( \Rightarrow \Delta ABC = \Delta XYZ\) (g.c.g)
+)Xét hai tam giác vuông DEF và GHK có:
\(EF = HK\) (gt)
\(\widehat {EFD} = \widehat {GKH}\) (gt)
\( \Rightarrow \Delta DEF = \Delta GHK\) (cạnh huyền – góc nhọn)
+)Xét hai tam giác vuông MNP và RTS có:
\(MN = TR\) (gt)
\(\widehat R = \widehat M( = 90^\circ )\) (gt)
\(PM = SR\) (gt)
\( \Rightarrow \Delta MNP = \Delta RTS\) (c.g.c)
QT
Hãy chỉ ra các cặp tam giác bằng nhau trong Hình 22 và cho biết chúng bằng nhau theo trường hợp nào.
1
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
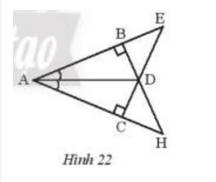
+) Xét \(\Delta{ABD}\) vuông tại B và \(\Delta{ACD}\) vuông tại D có:
AD chung
\(\widehat {BAD} = \widehat {DAC}\) (gt)
\( \Rightarrow \Delta{ABD}=\Delta{ACD}\) (cạnh huyền – góc nhọn)
\( \Rightarrow \) BD = CD, AB = AC ( 2 cạnh tương ứng)
\( \widehat {BDA} = \widehat {ADC}\)( 2 góc tương ứng)
+) Xét \(\Delta{BED}\) vuông tại B và \(\Delta{CHD}\) vuông tại C có:
BD = CD (cmt)
\(\widehat {BDE} = \widehat {CDH}\)( 2 góc đối đỉnh )
\( \Rightarrow \Delta{BED}=\Delta{CHD \) (cạnh góc vuông - góc nhọn kề )
+) Ta có: \(\widehat {BDA} + \widehat {BDE}\)= \(\widehat {ADE}\)
\(\widehat {ADC} + \widehat {CDH}\)= \(\widehat {ADH}\)
Mà \(\widehat {BDA} = \widehat {ADC}\), \(\widehat {BDE} = \widehat {CDH}\)
\( \Rightarrow \widehat {ADE} = \widehat {ADH}\)
Xét \(\Delta{ADE}\) và \(\Delta{ADH}\) có:
\(\widehat {BAD} = \widehat {DAC}\) (gt)
AD chung
\(\widehat {ADE} = \widehat {ADH}\) (cmt)
\( \Rightarrow \Delta{ADE}=\Delta{ADH}\)( g – c – g )
+) Xét \(\Delta{ABH}\) vuông tại B và \(\Delta{ACE}\) vuông tại C có:
AB = AC (cmt)
\(\widehat {BAH}\) chung
\( \Rightarrow \Delta{ABH}=\Delta{ACE}\) (cạnh góc vuông – góc nhọn kề)
QT
Hãy chỉ ra các cặp tam giác bằng nhau trong Hình 13 và cho biết chúng bằng nhau theo trường hợp nào.
1
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
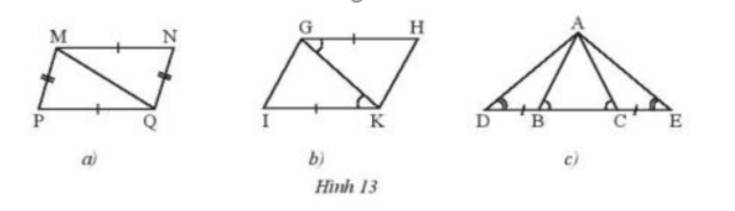
a) Ta thấy tam giác MNQ = tam giác MPQ (c-c-c)
b) Ta thấy tam giác GHK = tam giác GIK (c-g-c)
c) Ta thấy tam giác ADB = tam giác ACE (g-c-g)
Tam giác ADC = tam giác AEB (g-c-g)
CM
17 tháng 4 2018
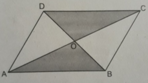
Xem hình bs.52.
- Các tam giác ADB, ACB, DAC, DBC có diện tích bằng nhau vì cùng bằng nửa diện tích hình bình hành đã cho.
- Các tam giác OAD, OCB, ODC, OBA có diện tích bằng nhau vì cùng bằng một phần tư diện tích hình bình hành đã cho.
C
3 tháng 5 2017
Ta có:
* SADB=SACB=SDAC=SDBC ( cùng bằng \(\dfrac{1}{2}.S_{hbh}\) )
* SOAD=SOCB=SODC=SOBA (cùng bằng \(\dfrac{1}{4}.S_{hbh}\))
CM
19 tháng 8 2019
- △ ABC đồng dạng △ HBA
Hai tam giác vuông có góc nhọn ở đỉnh B chung
- △ ABC đồng dạng △ HAC
Hai tam giác vuông có góc nhọn ở đỉnh C chung
- △ ABC đồng dạng △ NMC
Hai tam giác vuông có góc nhọn ở đỉnh C chung
- △ HAC đồng dạng △ NMC
Hai tam giác vuông có góc nhọn ở đỉnh C chung
- △ HAC đồng dạng △ HBA
Hai tam giác vuông có góc nhọn ∠ (HBA) = ∠ (HAC)
- △ HAB đồng dạng △ NCM
Hai tam giác vuông có góc nhọn ∠ (HAB) = ∠ (NCM)
a)Xét \(\Delta ABD\) và \(\Delta CDB\) có:
AB=CD (gt)
\(\widehat {ABD} = \widehat {CDB}\) (gt)
BD chung
Vậy \(\Delta ABD = \Delta CDB\)(c.g.c)
b)Xét \(\Delta OAD\) và \(\Delta OCB\) có:
AO=CO (gt)
\(\widehat {AOD} = \widehat {COB}\) (đối đỉnh)
OD=OB (gt)
Vậy \(\Delta OAD = \Delta OCB\)(c.g.c)