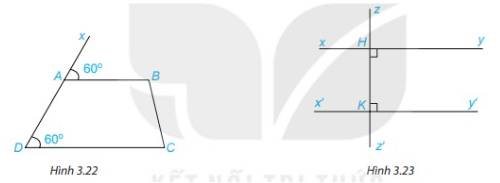
1. Quan sát Hình 3.22 và giải thích vì sao AB // CD.
2. Tìm trên Hình 3.23 hai đường thẳng song song với nhau và giải thích vì sao chúng song song?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có b không thuộc mặt phẳng (P) và b // a, a nằm trong (P). Nên b// (P).
b) Ta có p không thuộc sàn nhà và đường thẳng p song song với đường thẳng q trong sàn nhà nên p song song với sàn nhà.

a) Ta có b không thuộc mặt phẳng (P) và b // a, a nằm trong (P). Nên b// (P).
b) Ta có p không thuộc sàn nhà và đường thẳng p song song với đường thẳng q trong sàn nhà nên p song song với sàn nhà.

a) Xét hình 13a) : MN // AB.
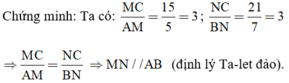
⇒ MN // AB (Theo định lý Ta-let đảo).
b) Xét hình 13b) : AB // A’B’ // A”B”.
Ta có: 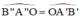
⇒ A’B’ // A”B” (Hai góc so le trong bằng nhau).
Lại có:
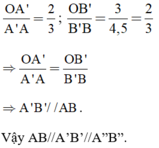

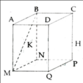
a) BB' và A'D' chéo nhau, CD và B'C' chéo nhau.
b) AB song song với CD (hoặc A'B')
c) (ABB'A') cắt (BDD'B') theo giao tuyến BB', (ABB'A')// (CDD'C') vì AB và AA' song song với (CDD'C').

Trên hình 13a ta có:
= ; = = vì ≠ nên ≠ => PM và MC không song song.
Ta có => MN//AB
Trong hình 13b
Ta có: = ; = =
=>

Ta thấy hai đường thẳng trên không có điểm chung với nhau nên chúng song song


a) Vì \(\widehat {{A_1}} = \widehat {{B_1}}( = 124^\circ )\). Mà 2 góc này ở vị trí so le trong nên z // t
b) Vì \(\widehat {{D_1}}= \widehat {{C_1}} (= 90^\circ) \)
Mà 2 góc này ở vị trí đồng vị nên m // n
c) Vì \(\widehat {{E_1}} + \widehat {{E_2}} = 180^\circ \) ( 2 góc kề bù) nên \(110^\circ + \widehat {{E_2}} = 180^\circ \Rightarrow \widehat {{E_2}} = 180^\circ - 110^\circ = 70^\circ \)
Vì \(\widehat {{E_2}} = \widehat {{G_1}}( = 70^\circ )\). Mà 2 góc này ở vị trí so le trong nên x // y
d) Vì \(\widehat {{K_1}} + \widehat {{K_2}} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {{K_1}} + 56^\circ = 180^\circ \Rightarrow \widehat {{K_1}} = 180^\circ - 56^\circ = 124^\circ \)
Vì \(\widehat {{H_1}} = \widehat {{K_1}}( = 124^\circ )\). Mà 2 góc này ở vị trí so le trong nên u // v
1. Vì \(\widehat {BAx} = \widehat {CDA}( = 60^\circ )\)
Mà 2 góc này ở vị trí đồng vị
\( \Rightarrow \) AB//CD (Dấu hiệu nhận biết hai đường thẳng song song)
2. Ta có: \(\widehat {zKy'} + \widehat {y'Kz'} = 180^\circ \) ( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow 90^\circ + \widehat {y'Kz'} = 180^\circ \\ \Rightarrow \widehat {y'Kz'} = 180^\circ - 90^\circ = 90^\circ \end{array}\)
Vì \(\widehat {yHz'} = \widehat {y'Kz'}\)
Mà 2 góc này ở vị trí đồng vị
\( \Rightarrow \) xy // x’y’ (Dấu hiệu nhận biết hai đường thẳng song song)
Chú ý:
2 đường thẳng cùng vuông góc với 1 đường thẳng thứ ba thì 2 đường thẳng đó song song.