Cho tam giác ABC có \(AB = 2\)cm, \(BC = 4\)cm. So sánh hai cạnh AC và AB.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 12 2021
bài 2:
ta có: AB<AC<BC(Vì 3cm<4cm<5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
LN
Lưu Nguyễn Hà An
CTVHS
15 tháng 2 2022
bài 2:
ta có: AB <AC <BC (Vì 3cm <4cm <5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
HT mik làm giống bạn Dương Mạnh Quyết
29 tháng 7 2023
a: Xét ΔABC có AB<AC<BC
nên góc C<góc B<góc A
b: góc C=180-50-60=70 độ
Xét ΔABC có góc A<góc B<góc C
nên BC<AC<AB
25 tháng 3 2023
a: AB<AC<BC
=>góc C<gócB<góc A
b: Xét ΔABD và ΔEBD có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
c,d: ΔBAD=ΔBED
=>góc ADB=góc EDB và góc BAD=góc BED=90 độ
=>DB là phân giác của góc ADE và DE vuông góc BC
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Theo đề bài ta có AB = 4cm, BC = 7cm, AC = 6cm
Có góc đối diện với cạnh AB là góc C, góc A đối diện với cạnh BC, góc B đối diện với cạnh AC
Theo định lí về góc đối diện với cạnh lớn hơn thì lớn hơn ta có :
\( \Rightarrow \widehat A > \widehat B > \widehat C\)
b)
Vì \(\widehat{A}=\widehat{C}\) nên tam giác ABC cân tại B
\( \Rightarrow BA = BC\)
Áp dụng định lí tổng 3 góc trong tam giác ABC, có:
\( \Rightarrow \widehat B = {180^o} - {100^0} = {80^o}\)
\( \Rightarrow \widehat B > \widehat A=\widehat C\)
\( \Rightarrow AC\) là cạnh lớn nhất tam giác ABC (Quan hệ giữa góc và cạnh đối diện trong tam giác)
KV
17 tháng 9 2023
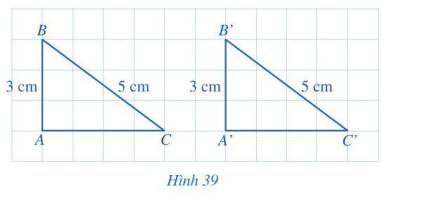
Xét hai tam giác vuông: ∆ABC và ∆A'B'C' có:
BC = B'C' = 5 cm
AB = A'B' = 3 cm
⇒ ∆ABC = ∆A'B'C' (cạnh huyền - cạnh góc vuông)
⇒ AC = A'C' (hai cạnh tương ứng)
23 tháng 7 2021
Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=15^2-9^2=144\)
hay AC=12(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\\CH=\dfrac{12^2}{15}=\dfrac{144}{15}=9,6\left(cm\right)\end{matrix}\right.\)
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AH^2+HB^2=AB^2\)
\(\Leftrightarrow AH^2=9^2-5.4^2=51,84\)
hay AH=7,2(cm)
Ta có: \(BC - AC = 4 - 2 = 2\).
Vậy độ dài cạnh AC lớn hơn 2 hay AC > AB (vì\(AB = 2\)cm).