Quan sát Hình 6. Vẽ vào tờ giấy tam giác \(DEF\) với \(EF = 4cm,\widehat E = 36^\circ ,\widehat F = 76^\circ \).a) Chứng minh \(\Delta DEF\backsim\Delta AMC\).b) Dùng thước đo chiều dài cạnh \(DF\) của \(\Delta DEF\). Tính khoảng cách giữa hia điểm \(A\) và \(C\) ở hai bờ sông trong Hình...
Đọc tiếp
Quan sát Hình 6. Vẽ vào tờ giấy tam giác \(DEF\) với \(EF = 4cm,\widehat E = 36^\circ ,\widehat F = 76^\circ \).
a) Chứng minh \(\Delta DEF\backsim\Delta AMC\).
b) Dùng thước đo chiều dài cạnh \(DF\) của \(\Delta DEF\). Tính khoảng cách giữa hia điểm \(A\) và \(C\) ở hai bờ sông trong Hình 6.
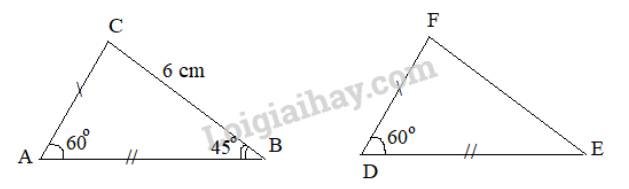
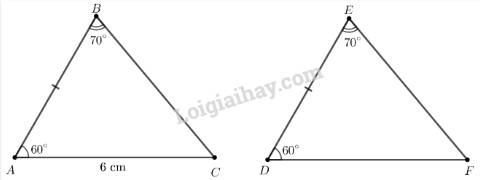
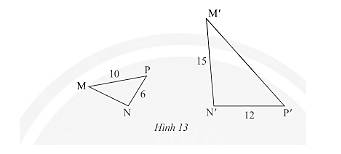
a) Xét tam giác \(DEF\) và tam giác \(AMC\) có:
\(\widehat E = \widehat M = 36^\circ \)
\(\widehat F = \widehat C = 76^\circ \) (chứng minh trên)
Suy ra, \(\Delta DEF\backsim\Delta AMC\) (g.g).
b) Đổi 25m = 2500 cm.
Dùng thước đo độ dài cạnh \(DF\) ta được độ dài \(DF\) là 2,6cm.
Vì \(\Delta DEF\backsim\Delta AMC\) nên \(\frac{{DF}}{{EF}} = \frac{{AC}}{{MC}}\) (hai cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{2,6}}{4} = \frac{{AC}}{{2500}} \Rightarrow AC = \frac{{2,6.2500}}{4} = 1625\).
Vậy khoảng cách giữa hai điểm \(A\) và \(C\) là 1625 cm hay 16,25m.