Cho tam giác \(ABC\)nhọn có hai đường cao \(BE,CF\) cắt nhau tại \(H\). Chứng minh rằng
a) \(\Delta AEB\backsim\Delta AFC\).
b) \(\frac{{HE}}{{HC}} = \frac{{HF}}{{HB}}\).
c) \(\Delta HEF\backsim\Delta HCB\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

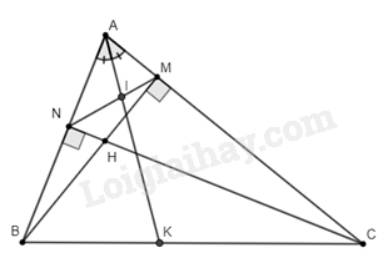
a) Vì \(BM\)là đường cao nên \(\widehat {AMB} = 90^\circ \); vì \(CN\)là đường cao nên \(\widehat {ANC} = 90^\circ \)
Xét tam giác \(AMB\) và tam giác \(ANC\) có:
\(\widehat A\) (chung)
\(\widehat {ANB} = \widehat {ANC} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta AMB\backsim\Delta ANC\) (g.g).
Suy ra, \(\frac{{AM}}{{AN}} = \frac{{AB}}{{AC}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Do đó, \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) (tỉ lệ thức)
Xét tam giác \(AMN\) và tam giác \(ABC\) có:
\(\widehat A\) (chung)
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) (chứng minh trên)
Suy ra, \(\Delta AMN\backsim\Delta ABC\) (c.g.c).
b) Xét tam giác \(AMN\) có \(AI\) là đường phân giác của \(\widehat {MAN}\left( {I \in MN} \right)\).
Theo tính chất đường phân giác ta có:
\(\frac{{IM}}{{IN}} = \frac{{AM}}{{AN}}\)
Xét tam giác \(ABC\) có \(AK\) là đường phân giác của \(\widehat {BAC}\left( {K \in BC} \right)\).
Theo tính chất đường phân giác ta có:
\(\frac{{BK}}{{KC}} = \frac{{AB}}{{AC}}\)
Mà \(\frac{{AM}}{{AN}} = \frac{{AB}}{{AC}}\) (chứng minh trên) nên \(\frac{{IM}}{{IN}} = \frac{{KB}}{{KC}}\) (điều phải chứng minh).

a) Xét tam giác ACD và tam giác BCE có:
\(\widehat {ADC} = \widehat {BEC} = 90^\circ ;\,\,\widehat C\) chung
\( \Rightarrow \Delta ACD \backsim \Delta BCE\) (g-g)
\( \Rightarrow \frac{{CA}}{{CB}} = \frac{{CD}}{{CE}}\) (Tỉ số đồng dạng) \( \Rightarrow CA.CE = CB.CD\)
b) Xét tam giác ACD và tam giác AHE có:
\(\widehat {ADC} = \widehat {AEH} = 90^\circ ;\,\,\widehat A\) chung
\( \Rightarrow \Delta ACD \backsim \Delta AHE\) (g-g)
\( \Rightarrow \frac{{AC}}{{AH}} = \frac{{AD}}{{AE}}\) (Tỉ số đồng dạng)
\( \Rightarrow AC.AE = AD.AH\)

\(BE||DM\) (cùng vuông góc AC)
Theo định lý Talet: \(\left\{{}\begin{matrix}\dfrac{MK}{EH}=\dfrac{CK}{CH}\\\dfrac{DK}{BH}=\dfrac{CK}{CH}\end{matrix}\right.\) \(\Rightarrow\dfrac{MK}{EH}=\dfrac{DK}{BH}\)
\(\Rightarrow\dfrac{BH}{EH}=\dfrac{DK}{MK}\)
Hai tam giác vuông AHE và ACD đồng dạng (chung góc A) \(\Rightarrow\dfrac{AH}{AC}=\dfrac{AE}{AD}\Rightarrow AH.AD=AC.AE\)
Tương tự CHE đồng dạng CAF \(\Rightarrow\dfrac{CH}{AC}=\dfrac{CE}{CF}\Rightarrow CH.CF=AC.CE\)
\(\Rightarrow AH.AD+CH.CF=AC.AE+AC.CE=AC\left(AE+CE\right)=AC^2\) (1)
Lại có 2 tam giác vuông ACD và DCM đồng dạng (chung góc C)
\(\Rightarrow\dfrac{AC}{CD}=\dfrac{CD}{CM}\Rightarrow AC=\dfrac{CD^2}{CM}\Rightarrow AC^2=\dfrac{CD^4}{CM^2}\) (2)
(1); (2) suy ra đpcm

a: Xét ΔAEB vuông tại E và ΔAFC vuôg tại F có
góc BAE chung
=>ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE*AC=AB*AF
b: Xét tứ giác AFHE có
góc AFH+góc AEH=180 độ
=>AFHE nội tiếp
=>góc FAH=góc FEH
=>goc BAD=góc BEF

hứng minh được , từ đó có .AE phần AB=AF phần AC
Ta có: (g.c.g)
b, từ câu a) suy ra EF phần BC=AE phần AB=cos A=cos60 độ =1 phần 2
=> BC=10cm
c) Saef phần Sabc=(AE phần AB)^2=cos^2 A=1 phần 4 => SAEF =1 phần 4 SABC=25cm^2

Lời giải:
câu c)
Ta có: \(\frac{HD}{AD}=\frac{HD.BC}{AD.BC}=\frac{2S_{BHC}}{2S_{ABC}}=\frac{S_{HBC}}{S_{ABC}}\)
\(\frac{HE}{BE}=\frac{HE.AC}{BE.AC}=\frac{2S_{AHC}}{2S_{ABC}}=\frac{S_{AHC}}{S_{ABC}}\)
\(\frac{HF}{CF}=\frac{HF.AB}{CF.AB}=\frac{2S_{AHB}}{2S_{ABC}}=\frac{S_{AHB}}{S_{ABC}}\)
Cộng theo vế các đẳng thức vừa thu được:
\(\frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}=\frac{S_{HBC}+S_{AHC}+S_{AHB}}{S_{ABC}}=\frac{S_{ABC}}{S_{ABC}}=1\)
Ta có đpcm.

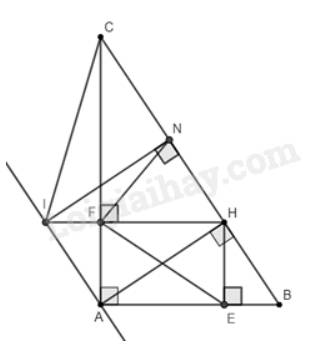
a) Vì \(AH\) là đường cao nên \(\widehat {AHB} = \widehat {AHC} = 90^\circ \)
Xét tam giác \(ABH\) và tam giác \(CBA\) có:
\(\widehat B\) (chung)
\(\widehat {AHB} = \widehat {CAB} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta ABH\backsim\Delta CBA\) (g.g).
Do đó, \(\frac{{AB}}{{CB}} = \frac{{BH}}{{AB}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra, \(A{B^2} = BH.BC\) .
b)
- Vì \(HE\) vuông góc với \(AB\) nên \(\widehat {HEA} = \widehat {HEB} = 90^\circ \)
Xét tam giác \(AHE\) và tam giác \(ABH\) có:
\(\widehat {HAE}\) (chung)
\(\widehat {HEA} = \widehat {AHB} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta AHE\backsim\Delta ABH\) (g.g).
Do đó, \(\frac{{AH}}{{AB}} = \frac{{AE}}{{AH}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra, \(A{H^2} = AB.AE\) . (1)
- Vì \(HF\) vuông góc với \(AC\) nên \(\widehat {HFC} = \widehat {HFA} = 90^\circ \)
Xét tam giác \(AHF\) và tam giác \(ACH\) có:
\(\widehat {HAF}\) (chung)
\(\widehat {AFH} = \widehat {AHC} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta AHF\backsim\Delta ACH\) (g.g).
Do đó, \(\frac{{AH}}{{AC}} = \frac{{AF}}{{AH}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra, \(A{H^2} = AF.AC\) . (2)
Từ (1) và (2) suy ra, \(AE.AB = AF.AC\) (điều phải chứng minh)
c) Vì \(AE.AB = AF.AC \Rightarrow \frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}\).
Xét tam giác \(AFE\) và tam giác \(ABC\) có:
\(\widehat A\) (chung)
\(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}\) (chứng minh trên)
Suy ra, \(\Delta AFE\backsim\Delta ABC\) (c.g.c).
d) Vì \(HF\) vuông góc với \(AC\) nên \(CF \bot HI\), do đó, \(\widehat {CFH} = \widehat {CFI} = 90^\circ \).
Vì \(IN \bot CH \Rightarrow \widehat {CBI} = \widehat {HNI} = 90^\circ \).
Xét tam giác \(HFC\) và tam giác \(HNI\) có:
\(\widehat {CHI}\) (chung)
\(\widehat {HFC} = \widehat {HNI} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta HFC\backsim\Delta HNI\) (g.g).
Suy ra, \(\frac{{HF}}{{HN}} = \frac{{HC}}{{HI}}\) (hai cặp cạnh tương ứng cùng tỉ lệ)
Do đó, \(\frac{{HF}}{{HC}} = \frac{{HN}}{{HI}}\).
Xét tam giác \(HNF\) và tam giác \(HIC\) có:
\(\widehat {CHI}\) (chung)
\(\frac{{HF}}{{HC}} = \frac{{HN}}{{HI}}\) (chứng minh trên)
Suy ra, \(\Delta HNF\backsim\Delta HIC\) (c.g.c).
a) Vì \(BE\)là đường cao nên \(\widehat {AEB} = 90^\circ \); vì \(CF\)là đường cao nên \(\widehat {AFC} = 90^\circ \)
Xét tam giác \(AEB\) và tam giác \(AFC\) có:
\(\widehat A\) (chung)
\(\widehat {AEB} = \widehat {AFC} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta AEB\backsim\Delta AFC\) (g.g).
b) Vì \(\Delta AEB\backsim\Delta AFC\) nên \(\widehat {ACF} = \widehat {ABE}\) (hai góc tương ứng) hay \(\widehat {ECH} = \widehat {FBH}\).
Xét tam giác \(HEC\) và tam giác \(HFB\) có:
\(\widehat {ECH} = \widehat {FBH}\) (chứng minh trên)
\(\widehat {CEH} = \widehat {BFH} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta HEC\backsim\Delta HFC\) (g.g).
Suy ra, \(\frac{{HE}}{{HF}} = \frac{{HC}}{{HB}}\) (các cặp cạnh tương ứng tỉ lệ)
Hay \(\frac{{HE}}{{HC}} = \frac{{HF}}{{HB}}\) (điều phải chứng minh).
c) Xét tam giác \(HEF\) và tam giác \(HCB\) có:
\(\widehat {FHE} = \widehat {BHC}\) (hai góc đối đỉnh)
\(\frac{{HE}}{{HC}} = \frac{{HF}}{{HB}}\) (chứng minh trên)
Suy ra, \(\Delta HEF\backsim\Delta HCB\) (c.g.c).