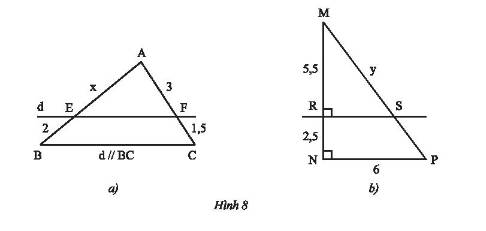
Tính độ dài \(x;y\) trong Hình 8.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 9 2021
\(1,\\ a,=\dfrac{7}{19}\times\left(\dfrac{1}{3}+\dfrac{2}{3}\right)=\dfrac{7}{19}\times1=\dfrac{7}{19}\\ b,=\dfrac{2}{5}+\left(\dfrac{3}{4}+\dfrac{1}{4}\right)=\dfrac{2}{5}+1=\dfrac{7}{5}\\ 2,\\ a,=15\times\left(\dfrac{2121}{4343}+\dfrac{222222}{434343}\right)\\ =15\times\left(\dfrac{2121:101}{4343:101}+\dfrac{222222:10101}{434343:10101}\right)\\ =15\times\left(\dfrac{21}{43}+\dfrac{22}{43}\right)=15\times\dfrac{43}{43}=15\times1=15\)
\(3,\)
Cạnh \(AC=\) chu vi ABC \(-AB-BC=\dfrac{4}{5}-\dfrac{1}{5}-\dfrac{1}{4}=\dfrac{3}{5}-\dfrac{1}{4}=\dfrac{7}{20}\left(m\right)\)
Vì \(\dfrac{7}{20}>\dfrac{5}{20}>\dfrac{4}{20}\Rightarrow\dfrac{7}{20}>\dfrac{1}{4}>\dfrac{1}{5}\) nên \(AC>BC>AB\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
21 tháng 10 2020
Đường trung bình của hình thang là NM
P, Q là giao của MN với BD và AC
\(\frac{AB}{CD}=\frac{2}{3}\)
\(EF=\frac{AB+CD}{2}\Rightarrow AB+CD=2.EF=2.5=10cm.\)
\(\Rightarrow AB=10:\left(2+3\right).2=4cm\Rightarrow CD=10-4=6cm\)
Xét tg ABD có
AN=DN
NP//AB
=> P là trung điểm của BD (trong 1 tg đường thẳng // với đáy và đi qua trung điểm 1 cạnh bên thì đi qua trung điểm cạnh bên còn lại)
=> NP là đường trung bình của tg ABD \(\Rightarrow NP=\frac{AB}{2}=\frac{4}{2}=2cm\)
Chứng minh tương tự khi xét tg ABC ta cũng c/m được Q là trung điểm của AC
Xét tg ADC có
AN=DN và AQ=CQ => NQ là đường trung bình của tg ADC \(\Rightarrow NQ=\frac{CD}{2}=\frac{6}{2}=3cm\)
Ta có PQ=NQ-NP=3-2=1 cm
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
a) Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{CD}}{{BD}} = \frac{{AC}}{{AB}} \Leftrightarrow \frac{x}{{2,4}} = \frac{5}{3} \Rightarrow x = \frac{{2,4.5}}{3} = 4\).
Vậy \(x = 4\).
b) Ta có: \(GH + HF = GF \Rightarrow HF = GF - GH = 20 - x\)
Vì \(EH\) là phân giác của góc \(GEF\) nên theo tính chất đường phân giác ta có:
\(\frac{{GH}}{{HF}} = \frac{{GE}}{{EF}} \Leftrightarrow \frac{x}{{20 - x}} = \frac{{18}}{{12}} \Leftrightarrow \frac{x}{{20 - x}} = \frac{3}{2} \Rightarrow 2x = 3.\left( {20 - x} \right)\)
\( \Leftrightarrow 2x = 60 - 3x \Leftrightarrow 5x = 60 \Rightarrow x = 12\)
Vậy \(x = 12\).
c) Vì \(RS\) là phân giác của góc \(RPQ\) nên theo tính chất đường phân giác ta có:
\(\frac{{PS}}{{SQ}} = \frac{{PR}}{{RQ}} \Leftrightarrow \frac{5}{6} = \frac{{10}}{x} \Rightarrow x = \frac{{10.6}}{5} = 12\).
Vậy \(x = 12\).
13 tháng 9 2023
a: Xét ΔABC có AD là phân giác
nên CD/AC=BD/AB
=>x/5=2,4/3=4/5
=>x=4
b: Xét ΔEGF có EH là phân giác
nên GH/HF=EG/EF
=>x/20-x=18/12=3/2
=>60-3x=2x
=>x=12
c: Xét ΔRPQ có RS là phân giác
nên PS/SQ=RP/RQ
=>10/x=5/6
=>x=12
13 tháng 9 2023
a: Xét ΔABC có MN//BC
nên AN/NC=AM/MB
=>x/7=2/4=1/2
=>x=3,5
b Xét ΔBDE có AC//DE
nên BA/BD=BC/BE
=>3/x=5/8,5=10/17
=>x=51/10
c: Xét ΔHIK có PQ//IK
nên HP/HI=HQ/HK
=>x/8=0,65
=>x=5,2
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
a) Xét tam giác \(ABC\) ta có \(MN//BC\), theo định lí Thales ta có:
\(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}} \Leftrightarrow \frac{2}{4} = \frac{x}{7} \Rightarrow x = \frac{{2.7}}{4} = 3,5\)
Vậy \(x = 3,5\).
b) Vì \(\left\{ \begin{array}{l}AC \bot BD\\DE \bot BD\end{array} \right. \Rightarrow AC//DE\)
Xét tam giác \(BDE\) ta có \(AC//DE\), theo định lí Thales ta có:
\(\frac{{AB}}{{BD}} = \frac{{BC}}{{BE}} \Leftrightarrow \frac{3}{x} = \frac{5}{{3,5 + 5}} \Rightarrow x = \frac{{3.\left( {3,5 + 5} \right)}}{5} = 5,1\)
Vậy \(x = 5,1\).
c) Xét tam giác \(HIK\) ta có \(PQ//IK\), theo định lí Thales ta có:
\(\frac{{HP}}{{HI}} = \frac{{HQ}}{{HK}} \Leftrightarrow \frac{x}{8} = \frac{{6,5}}{{6,5 + 3,5}} \Rightarrow x = \frac{{8.6,5}}{{\left( {6,5 + 3,5} \right)}} = 5,2\)
Vậy \(x = 5,2\).
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
a) Xét tam giác \(ABC\) có \(AD\) là đường phân giác của \(\widehat A\). Theo định lí đường phân giác ta có:
\(\frac{{BD}}{{AB}} = \frac{{DC}}{{AC}} \Leftrightarrow \frac{x}{{4,5}} = \frac{5}{{7,2}} \Rightarrow x = \frac{{4,5.5}}{{7,2}} = 3,125\)
Vậy \(x = 3,125\).
b) Xét tam giác \(MNP\) có \(MI\) là đường phân giác của \(\widehat M\). Theo định lí đường phân giác ta có: \(O\)
\(\frac{{NI}}{{MN}} = \frac{{IP}}{{MP}} \Leftrightarrow \frac{3}{5} = \frac{{IP}}{{8,5}} \Rightarrow IP = \frac{{3.8,5}}{5} = 5,125\)
Ta có: \(NP = NI + IP = 3 + 5,1 = 8,1\)
Vậy \(x = 8,1\).
PT
1
14 tháng 9 2021
Xét tam giác ABH vuông tại H có:
\(AH^2=AB^2-BH^2\left(Pytago\right)\)
\(\Rightarrow AH^2=15^2-12^2=81\Rightarrow AH=9\)
Xét tam giác AHC vuông tại H có:
\(HC^2=AC^2-AH^2\left(Pytago\right)\)
\(\Rightarrow x^2=41^2-9^2=1600\Rightarrow x=40\)
a)
Xét tam giác \(ABC\) có \(d//BC\) mà \(d\) cắt \(AB;AC\) lần lượt tại \(E\) và \(F\)nên theo định lí Thales ta có:
\(\frac{{AE}}{{BE}} = \frac{{AF}}{{CF}} \Rightarrow \frac{x}{2} = \frac{3}{{1,5}}\). Do đó, \(x = \frac{{2.3}}{{1,5}} = 4\).
Vậy \(x = 4\).
b) Ta có: \(MN = NR + MR = 2,5 + 5,5 = 8\)
Xét tam giác \(MNP\) vuông tại \(N\) ta có:
\(M{N^2} + N{P^2} = M{P^2}\)
\({8^2} + {6^2} = M{P^2}\)
\(100 = M{P^2} \Rightarrow MP = \sqrt {100} = 10\)
Xét tam giác \(MNP\) có \(\left\{ \begin{array}{l}RS \bot MN\\NP \bot MN\end{array} \right. \Rightarrow RS//NP\) (quan hệ từ vuông góc đến song song) nên theo định lí Thales ta có:
\(\frac{{MR}}{{MN}} = \frac{{MS}}{{MP}} \Rightarrow \frac{{5,5}}{8} = \frac{y}{{10}}\). Do đó, \(y = \frac{{5,5.10}}{8} = 6,875\).
Vậy \(y = 6,875\).