Cho tam giác ABC có góc A = góc B. Trên các cạnh CB, CA lần lượt lấy các điểm D, E sao cho CD = CE. Gọi F là giao điểm của AD và BE. Chứng minh FA = FB".
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


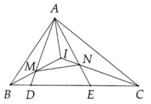
a) Tam giác ABE cân tại B có BI là phân giác nên cũng là đường cao, từ đó B I ⊥ A E . Tương tự C I ⊥ A D .
b) Từ kết quả ý a, chứng minh được I là trực tâm tam giác AMN, từ đó A I ⊥ M N

Bài 5:
Tgiac ABC vuông cân tại A => góc CBA = 45 độ
Xét góc CBA là góc ngoài tgiac DBC => góc CBA = góc D + DCB
Xét tgiac DBC có DB = BC => tgiac DBC cân tại B => góc D = góc DBC
=> góc D = 45/2 = 22,5 độ
và góc ACD = 22,5 + 45 = 67,5 độ
Vậy số đo các góc của tgiac ACD là ...
Bài 6:
Tgiac ABC cân tại B, góc B = 100 độ => góc A = góc C = 40 độ
Xét tgiac ABD có AB = AD => tgiac ABD cân tại A => góc EDB (ADB) = (180-40)/2 =70 độ
cmtt với tgiac CBE => góc DEB = 70 độ
=> góc DBE = 180-70-70 = 40 độ
Bài 7:
Xét tgiac ABC cân tại A => góc BAC = 180 - 2.góc C => 2.(90 - góc C)
Xét tgiac BHC vuông tại H => góc CBH = 90 - góc C
=> đpcm
Bài 8: mai làm hihi

a: Xét ΔABE và ΔACDcó
AB=AC
góc BAE chung
AE=AD
=>ΔABE=ΔACD
=>BE=CD
b: ΔABE=ΔACD
=>góc ABE=góc ACD
c: góc ABE+góc KBC=góc ABC
góc ACD+góc KCB=góc ACB
mà góc ABE=góc ACD và góc ABC=góc ACB
nên góc KBC=góc KCB
=>KB=KC
d: AB=AC
KB=KC
=>AK là trung trực của BC
=>A,K,I thẳng hàng

a: AC=12cm
Xét ΔABC có AB<AC<BC
nên \(\widehat{C}< \widehat{B}< \widehat{A}\)
b: Xét ΔCBD có
CA là đường cao
CA là đường trung tuyến
Do đó: ΔCBD cân tại C
Suy ra: CB=CD


Xét ΔCAB có góc CAB=góc CBA
nên ΔCAB cân tại C
=>CA=CB
CE+EA=CA
CD+DB=CB
mà CD=CE và CA=CB
nên EA=DB
Xét ΔEAB và ΔDBA có
EA=DB
góc EAB=góc DBA
BA chung
Do đó: ΔEAB=ΔDBA
=>góc EBA=góc DAB
=>góc FAB=góc FBA
=>FA=FB