Vẽ đồ thị hàm số các hàm số bậc nhất sau:
a) \(y = - 3{\rm{x}} + 3\)
b) \(y = \frac{1}{2}x - 4\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
27 tháng 9 2023
a)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
2. Nhập phương trình bậc hai theo cú pháp y=-x^2+4x-3 vào vùng nhập lệnh như hình bên
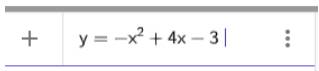
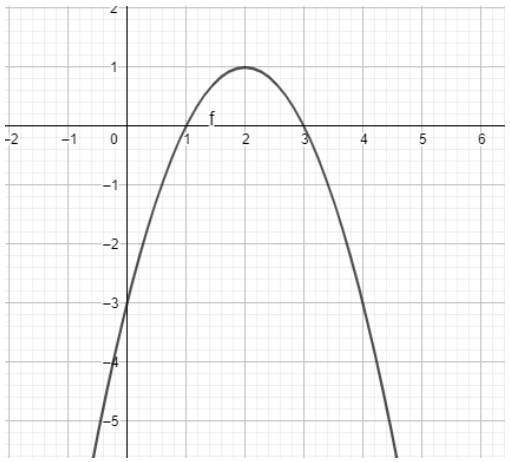
Ta có ngay parabol trên vùng làm việc như hình dưới:
b)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
2. Nhập phương trình bậc hai theo cú pháp y=x^2+2 vào vùng nhập lệnh như hình bên
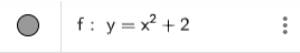
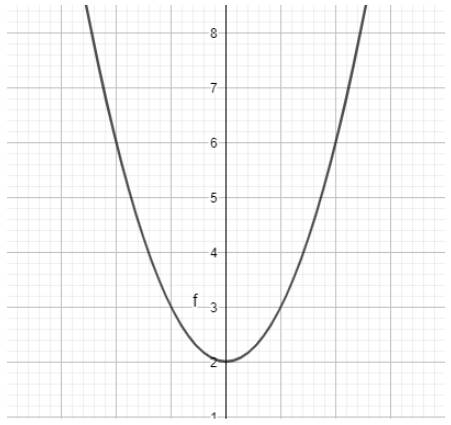
Ta có ngay parabol trên vùng làm việc như hình dưới:
c)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
2. Nhập phương trình bậc hai theo cú pháp y=1/2x^2+x+1 vào vùng nhập lệnh như hình bên
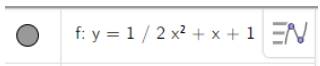
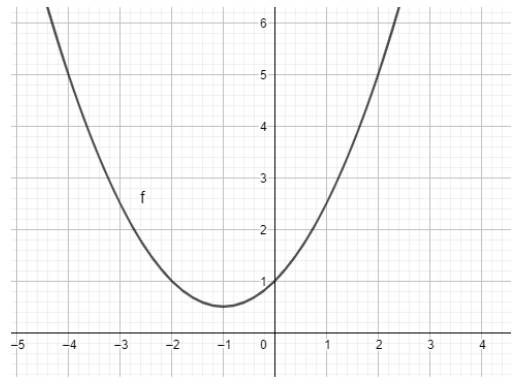
Ta có ngay parabol trên vùng làm việc như hình dưới:
d)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
2. Nhập phương trình bậc hai theo cú pháp y=x^2-4x+4 vào vùng nhập lệnh như hình bên
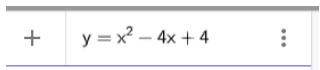
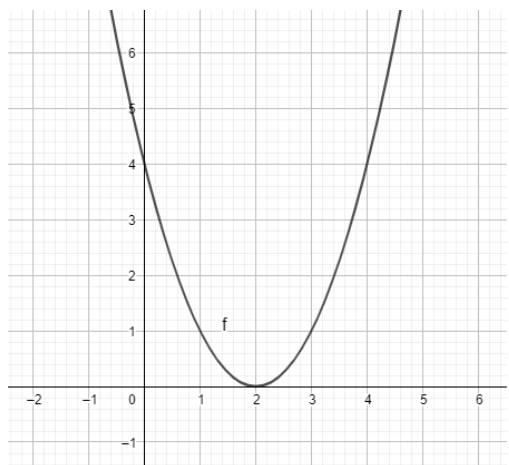
Ta có ngay parabol trên vùng làm việc như hình dưới:
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
a) \(y' = 2.3{{\rm{x}}^2} - \frac{1}{2}.2{\rm{x}} + 4.1 - 0 = 6{{\rm{x}}^2} - x + 4\).
b) \(y' = \frac{{{{\left( { - 2{\rm{x}} + 3} \right)}^\prime }.\left( {{\rm{x}} - 4} \right) - \left( { - 2{\rm{x}} + 3} \right).{{\left( {{\rm{x}} - 4} \right)}^\prime }}}{{{{\left( {{\rm{x}} - 4} \right)}^2}}}\)
\( = \frac{{ - 2\left( {{\rm{x}} - 4} \right) - \left( { - 2{\rm{x}} + 3} \right).1}}{{{{\left( {{\rm{x}} - 4} \right)}^2}}}\)
\( = \frac{{ - 2{\rm{x}} + 8 + 2{\rm{x}} - 3}}{{{{\left( {{\rm{x}} - 4} \right)}^2}}} = \frac{5}{{{{\left( {{\rm{x}} - 4} \right)}^2}}}\)
c) \(y' = \frac{{{{\left( {{x^2} - 2{\rm{x}} + 3} \right)}^\prime }\left( {{\rm{x}} - 1} \right) - \left( {{x^2} - 2{\rm{x}} + 3} \right){{\left( {{\rm{x}} - 1} \right)}^\prime }}}{{{{\left( {{\rm{x}} - 1} \right)}^2}}}\)
\( = \frac{{\left( {2{\rm{x}} - 2} \right)\left( {{\rm{x}} - 1} \right) - \left( {{x^2} - 2{\rm{x}} + 3} \right).1}}{{{{\left( {{\rm{x}} - 1} \right)}^2}}}\) \( = \frac{{2{{\rm{x}}^2} - 2{\rm{x}} - 2{\rm{x}} + 2 - {x^2} + 2{\rm{x}} - 3}}{{{{\left( {{\rm{x}} - 1} \right)}^2}}}\)
\( = \frac{{{x^2} - 2{\rm{x}} - 1}}{{{{\left( {{\rm{x}} - 1} \right)}^2}}}\)
d) \(y' = {\left( {\sqrt 5 .\sqrt x } \right)^\prime } = \sqrt 5 .\frac{1}{{2\sqrt x }} = \frac{{\sqrt 5 }}{{2\sqrt x }} = \frac{5}{{2\sqrt {5x} }}\).
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
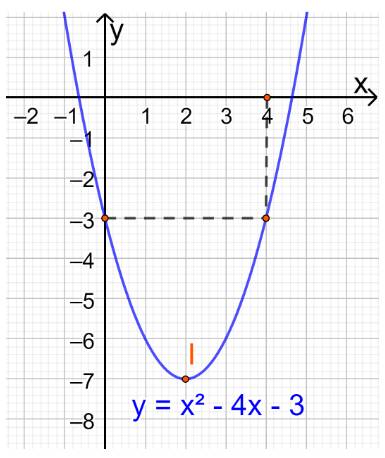
a) Đồ thị hàm số có đỉnh \(I\left( {2; - 7} \right)\)
Trục đối xứng là x=2
Giao điểm của parabol với trục tung là (0;-3)
Điểm đối xứng với điểm (0;-3) qua trục đối xứng x=2 là (4;-3)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
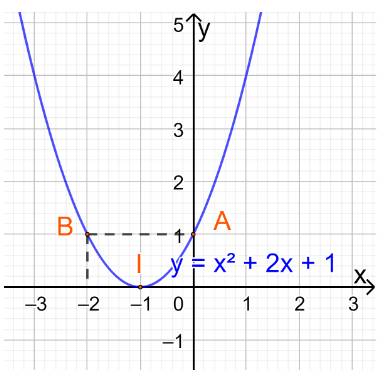
b) Đồ thị hàm số có đỉnh \(I\left( { - 1;0} \right)\)
Trục đối xứng là x=-1
Giao điểm của parabol với trục tung là (0;1)
Giao điểm của parabol với trục hoành là (-1;0)
Điểm đối xứng với điểm (0;1) qua trục đối xứng x=-1 là (-2;1)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
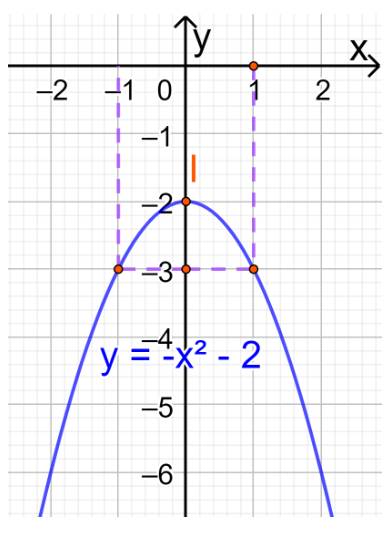
c) Đồ thị hàm số có đỉnh \(I\left( {0; - 2} \right)\)
Trục đối xứng là x=0
Giao điểm của parabol với trục tung là (0;-2)
Cho x=1=>y=-3
=> Điểm A(1;-3) thuộc đồ thị.
Điểm đối xứng với A qua trục đối xứng x=0 là điểm B(-1;-3).
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
B
1
20 tháng 8 2023
a, \(y=3x^4-7x^3+3x^2+1\)
\(y'=12x^3-21x^2+6x\)
b, \(y=\left(x^2-x\right)^3\)
\(y'=3\left(x^2-x\right)^2\left(2x-1\right)\)
c, \(y=\dfrac{4x-1}{2x+1}\)
\(y'=\dfrac{4+2}{\left(2x+1\right)^2}\)
\(y'=\dfrac{6}{\left(2x+1\right)^2}\)
20 tháng 8 2023
a: y=3x^4-7x^3+3x^2+1
=>y'=3*4x^3-7*3x^2+3*2x
=12x^3-21x^2+6x
b: \(y'=\left[\left(x^2-x\right)^3\right]'\)
\(=3\left(2x-1\right)\left(x^2-x\right)^2\)
c: \(y'=\dfrac{\left(4x-1\right)'\left(2x+1\right)-\left(4x-1\right)\left(2x+1\right)'}{\left(2x+1\right)^2}\)
\(=\dfrac{4\left(2x+1\right)-2\left(4x-1\right)}{\left(2x+1\right)^2}=\dfrac{6}{\left(2x+1\right)^2}\)
21 tháng 8 2023
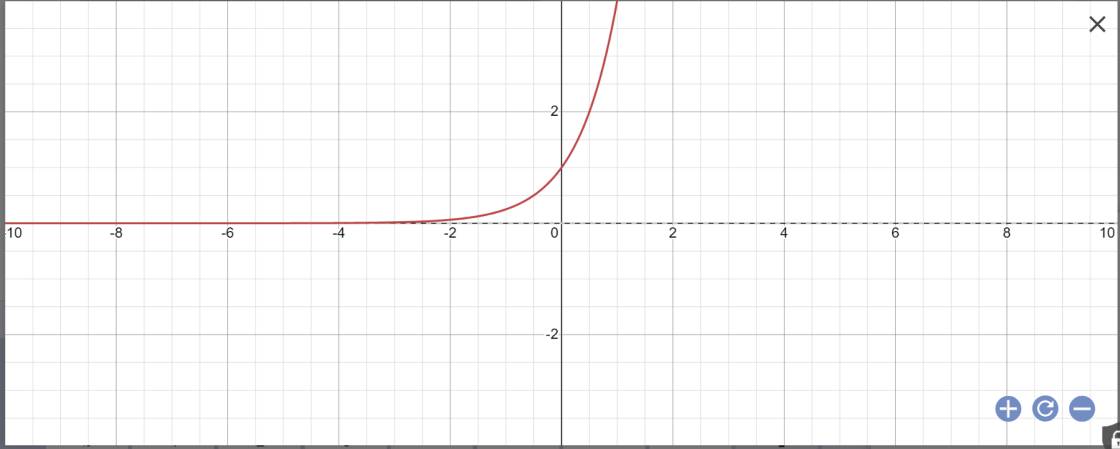
a:
Bảng giá trị:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 1/16 | 1/4 | 1 | 4 | 16 |
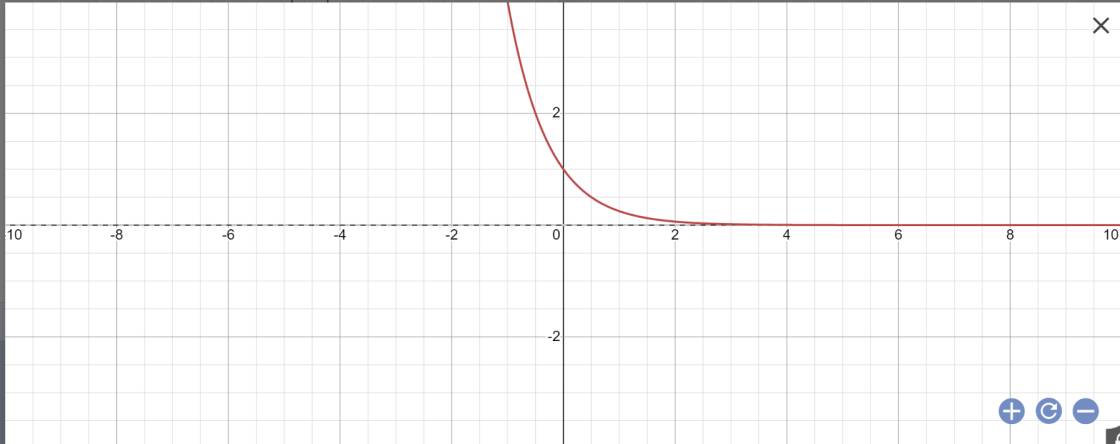
b:
Bảng giá trị:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 16 | 4 | 1 | 1/4 | 1/16 |
a) Nhập hàm số y = –3x + 3 trên ô lệnh, màn hình sẽ hiển thị đồ thị của hàm số.
b) Nhập hàm số y = \(\dfrac{1}{2}x-4\) trên ô lệnh, màn hình sẽ hiển thị đồ thị của hàm số