Các bạn giúp mik bài này với:
CHo tam giác ABC vuông tại A, đường cao AH. Vẽ HK _|_ AB ( K thuộc AB)
Chưng minh: a) AB .AK= HB.HC
b) \(\frac{AB^2}{AC^2}=\frac{HB}{HC}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 6 2016
a) ta có theo công thức lượng giác :
xét trong tam giác vuông AHB ta có AK.AB=AH2
mặt khác trong tam giác vuông ABC có : AH2=HC.HB
=> AK.AB=HB.HC (=AH2)
16 tháng 6 2016
a) tam giác AKH vuông tại K và tam giác AHB vuông tại H có
góc KAH =góc HAB
=> tam giác AKH đồng dạng tam giác AHB (g-g)
=> AK/AH=AH/AB
=> AH^2=AK.AB (1)
tam giác ABC vuông tại A=> AH^2=BH.CH (hệ thức lượng tam giác vuông )
(1),(2)=> AK.AB=BH.CH (đpcm)
b) đề sai bn nhé phải là cm AB^2/AC^2=HB/HC
ta có AB^2=BH.BC (hệ thức lượng tam giác vuông )
ta có AC^2=HC.BC (hệ thức lượng tam giác vuông )
=> \(\frac{AB^2}{AC^2}=\frac{BH.BC}{CH.BC}=\frac{BH}{CH}\left(đpcm\right)\)
PT
1
CM
2 tháng 10 2017
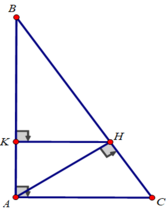
a) Xét tam giác ABC vuông tại A có đường cao AH
⇒ AH2 = HC.HB (1)
Xét tam giác AHB vuông tại H có đường cao HK
⇒ A H 2 = AK.AB (2)
Từ (1) và (2) ⇒ AK.AB = HC.HB
17 tháng 10 2021
a, Xét tam giác ABH vuông tại H, đường cao HG
Ta có : \(NH^2=AB.BG\)( hệ thức lượng )
b, Xét tam giác AHC vuông tại H, đường cao HK
Ta có : \(AH^2=AK.AC\)( hệ thức lượng ) (1)
Xét tam giác ABC vuông tại A, đường cao AH
Ta có : \(AH^2=HB.HC\)( hệ thức lượng ) (2)
Từ (1) ; (2) suy ra : \(AK.AC=HB.HC\Rightarrow\frac{AC}{HC}=\frac{HB}{AK}\)
7 tháng 4 2023
a: Xet ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
Xét ΔHAC vuông tại H và ΔABC vuông tại A có
góc C chung
=>ΔHAC đồng dạng vơi ΔABC
=>ΔHBA đồng dạng với ΔHAC
b: ΔHBA đồng dạng với ΔHAC
=>HB/HA=HA/HC
=>HA^2=HB*HC
c: AH=căn 9*16=12cm
AB=căn 9*25=15cm
=>AC=20cm
12 tháng 2 2023
a: Xét ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC
b: \(AH=\sqrt{9\cdot16}=12\left(cm\right)\)
\(AB=\sqrt{9\cdot25}=15\left(cm\right)\)
=>AC=20(cm)