Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A, B. Trên tia Oy lấy hai điểm C, D sao cho OA = OC, OB = OD.
a) Chứng minh AD = BC
b) Chứng minh \(\widehat{BAD}=\widehat{BCD}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 3 2023
`a)`
Xét `Delta OAD` và `Delta OCB` có :
`{:(OD=OB(GT)),(hat(O)-chung),(OA=OC(GT)):}}`
`=>Delta OAD=Delta OCB(c.g.c)(đpcm)`
`b)`
Có `Delta OAD=Delta OCB(cmt)=>hat(A_1)=hat(C_1)` ( 2 góc t/ứng )
mà `hat(A_1)+hat(A_2)=180^0` ( Kề bù )
`hat(C_1)+hat(C_2)=180^0` ( Kề bù )
nên `hat(A_2)=hat(C_2)(đpcm)`
`c)`
Có `Delta OAD=Delta OCB(cmt)=>hat(D_1)=hat(C_1)` ( 2 góc t/ứng )
Có `OA = OC;OB = OD(GT)`.
`=>OB-OA=OD-OC`
hay `AB=CD`
Xét `Delta AKB` và `Delta `CKD` có :
`{:(hat(B_1)=hat(D_1)(cmt)),(AB=CD(cmt)),(hat(A_2)=hat(C_2)(cmt)):}}`
`=>Delta AKB=Delta CKD(g.c.g)(đpcm)`
10 tháng 7 2017
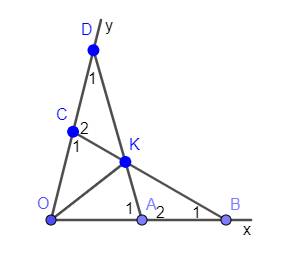
a) Xét \(\Delta OAD\) và \(\Delta OCB\) có:
OA = OC (gt)
\(\widehat{O}\) (chung)
OB = OD(gt)
Do đó: \(\Delta OAD=\Delta OCB\left(c-g-c\right)\)
=> AD = BC (hai cạnh tương ứng)
b) Vì \(\Delta OAD=\Delta OCB\left(cmt\right)\)
=> \(\widehat{OAD}=\widehat{OCB}\) (hai góc tương ứng)
mà :
\(\widehat{OAD}+\widehat{BAD}=180^0\) (kề bù)
\(\widehat{OCB}+\widehat{BCD}=180^0\) (kề bù)
=> \(\widehat{BAD}=\widehat{BCD}\) (đpcm)
CM
5 tháng 3 2019
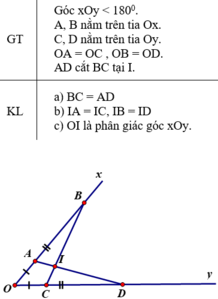
a) ΔAOD và ΔCOB có:
OA = OC (giả thiết)
Góc O chung
OD = OB (giả thiết)
⇒ ΔAOD = ΔCOB (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)
CM
3 tháng 1 2019
Ta có: ΔOIA và ΔOIC có
OI chung
IA = IC (chứng minh trên)
OA = OC (giả thiết)
ΔOIA = ΔOIC (c.c.c)
CM
30 tháng 12 2018
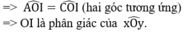
- ΔAOD = ΔCOB
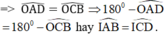
Lại có: OA = OC, OB = OD ⇒ OB – OA = OD – OC hay AB = CD.
- Xét ΔDIC và ΔBIA có:
CD = AB (chứng minh trên)
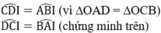
⇒ ΔDIC = ΔBIA (g.c.g)
⇒ IC = IA và ID = IB (các cặp cạnh tương ứng)
R
27 tháng 1 2022
a)
ΔOAD và ΔOCB có:
OA = OC (gt)
Góc O chung
OD = OB (gt)
⇒ ΔOAD = ΔOCB (c.g.c)
⇒ AD = BC (hai cạnh tương ứng).
27 tháng 1 2022
c) Ta có:
ΔEAB=ΔECD
nên EB=ED
Xét ΔOEB và ΔOED có
OE chung
EB=ED
OB=OD
Do đó: ΔOEB=ΔOED
Suy ra: BOE=DOE
hay OE là tia phân giác của góc xOy