Cho tam giác ABC vuông tại A,gọi M la trung điểm BC.CM :MA=\(\frac{1}{2}BC\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
0
EC
0
H
2
13 tháng 7 2015
Tam giác vuông ABC, vuông tại A, có AM là trung tuyến
trên tia đối của MA lấy điểm D sao cho MD=AM
Do đó AM=1/2 AD (1)
suy ra tứ giác ABDC là hình bình hành, có ^A=90*
nên ABDC là hình chữ nhật
suy ra AD=BC (2)
Từ (1) và (2) ta có AM => 1/2 BC
13 tháng 7 2015
Tam giác vuông ABC, vuông tại A, có AM là trung tuyến
trên tia đối của MA lấy điểm D sao cho MD=AM
Do đó AM=1/2 AD (1)
suy ra tứ giác ABDC là hình bình hành, có ^A=90*
nên ABDC là hình chữ nhật
suy ra AD=BC (2)
Từ (1) và (2) ta có AM = 1/2 BC (đpcm)
LT
1
4 tháng 8 2021
\(BM=CM=\frac{1}{2}BC\)
Mà BM=CM=AM
\(\Rightarrow AM=\frac{1}{2}BC\)(1)
Trong tam giác vuông đường trung tuyến ứng với cạnh huyền thì bằng một nửa cạnh huyền nên ta có:
M là trung điểm của BC nên AM là đường trung tuyến (2)
Từ (1) và (2) ta có ;
\(\Delta ABC\)vuông tại A
AH
Akai Haruma
Giáo viên
26 tháng 12 2022
Lời giải:
a.
Xét tam giác $AMB$ và $EMC$ có:
$\widehat{AMB}=\widehat{EMC}$ (đối đỉnh)
$AM=EM$
$MB=MC$
$\Rightarrow \triangle AMB=\triangle EMC$ (c.g.c)
b.
Vì $\triangle AMB=\triangle EMC$ nên $\widehat{MAB}=\widehat{MEC}$
Mà 2 góc này ở vị trí so le trong nên $EC\parallel AB$
Mà $AB\perp AC$ nên $EC\perp AC$ (đpcm)
c.
Vì $\triangle AMB=\triangle EMC$ nên:
$AB=EC$
Vì $EC\perp AC$ nên $\widehat{ECA}=90^0=\widehat{BAC}$
Xét tam giác $ECA$ và $BAC$ có:
$\widehat{ECA}=\widehat{BAC}=90^0$ (cmt)
$AC$ chung
$EC=BA$ (cmt)
$\Rightarrow \triangle ECA=\triangle BAC$ (c.g.c)
$\Rightarrow EA=BC$
Mà $EA=2AM$ nên $2AM=BC$ (đpcm)
30 tháng 11 2023
a: Xét ΔMAB và ΔMEC có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)
MB=MC
Do đó: ΔMAB=ΔMEC
b: ΔMAB=ΔMEC
=>\(\widehat{MAB}=\widehat{MEC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//EC
c: AB//EC
AB\(\perp\)AC
Do đó: EC\(\perp\)AC tại C
Xét ΔMAC và ΔMEB có
MA=ME
\(\widehat{AMC}=\widehat{EMB}\)
MC=MB
Do đó: ΔMAC=ΔMEB
=>\(\widehat{MAC}=\widehat{MEB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BE
AC//BE
AC\(\perp\)CE
Do đó: BE\(\perp\)CE
=>ΔBEC vuông tại E
T
1 tháng 8 2019
#)Giải : (Hình tự vẽ lười lắm òi)
Vì \(AB//CD\Rightarrow\widehat{BAC}+\widehat{ACD}=180^o=90^o+\widehat{ACD}=180^o\Rightarrow\widehat{ACD}=90^o\)
Ta có : \(\widehat{BAC}=\widehat{ACD}\)
\(AB=CD\left(c/m\Delta ABM=\Delta CDM\right)\)
AC là cạnh chung
\(\Rightarrow\Delta ABC=\Delta ACD\left(c.g.c\right)\)
\(\Rightarrow AD=BC\)
Mà \(AM=\frac{1}{2}AD\Rightarrow AM=\frac{1}{2}BC\)
CC
1 tháng 8 2019
M là trung điểm AD => AM = 1/2 AD (1)
và AM = MD
Xét ∆AMB và ∆AMC có :
AM = MD (cmt)
\(\widehat{AMB}=\widehat{AMC}\)( đối đỉnh)
MB = MC (M là trung điểm BC)
do đó ∆AMB = ∆AMC (c-g-c)
=> AB = AC và \(\widehat{B_1}=\widehat{C_1}\)
Mà \(\widehat{B_1};\widehat{C_1}\)ở vị trí so le trong
=> AB // CD
=> \(\widehat{BAC}+\widehat{ACD}=180^o\)( trong cùng phía)
Mà \(\widehat{BAC}=90^o\Rightarrow\widehat{ACD}=90^o\Rightarrow\widehat{BAC}=\widehat{ACD}\)
Xét ∆ABC và ∆CDA có :
AB = AC (cmt)
\(\widehat{BAC}=\widehat{ACD}\)
AC chung
do đó : ∆ABC = ∆CDA
=> BC = AD (2)
Từ (1),(2) => đpcm
10 tháng 2 2021
a , Xét \(\Delta AMC\)và \(\Delta DMB\)có :
BM = MC ( M là trung điểm của BC )
AM = MD ( giả thiết )
\(\widehat{AMC}=\widehat{BMD}\)( đối đỉnh )
=> \(\Delta AMC\)= \(\Delta DMB\) ( c.g.c )
=> BM = MA ( 2 cạnh tương ứng ) ; \(\widehat{MCA}=\widehat{MDB}\) ( 2 góc tương ứng )
b , Vì \(\widehat{MCA}=\widehat{MDB}\)= > \(\widehat{ADB}=\widehat{BCA}\)
Vì BM = MA => \(\Delta AMB\)cân tại M .
=> \(\widehat{MAB}=\widehat{MBA}\)
Ta có : \(\widehat{ABC}+\widehat{ACB}=90^0\)( \(\Delta ABC\perp A\))
hay \(\widehat{ABM}+\widehat{ACM}=90^0\)
vì \(\widehat{MCA}=\widehat{MDB}\); \(\widehat{MAB}=\widehat{MBA}\)
=> \(\widehat{BAM}+\widehat{BDM}=90^0\)
=> \(\widehat{BAD}=90^0\)
c , Vì AM = BM
mà BM = \(\frac{1}{2}BC\)
=> AM = \(\frac{1}{2}BC\)
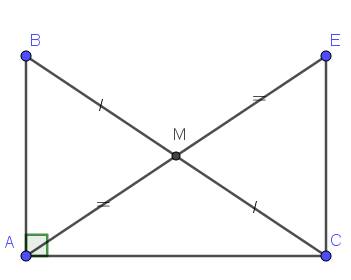
Tam giác vuông ABC, vuông tại A, có AM là trung tuyến
trên tia đối của MA lấy điểm D sao cho MD=AM
Do đó AM=1/2 AD (1)
suy ra tứ giác ABDC là hình bình hành, có ^A=90*
nên ABDC là hình chữ nhật
suy ra AD=BC (2)
Từ (1) và (2) ta có AM = 1/2 BC