Tính diện tích xung quanh của hình chóp ∆ đều có cạnh đáy 2,3cm và chiều cao của mặt bên xuất phát từ đỉnh của hình chóp ∆ đều bằng 2,5cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
a) Diện tích xung quanh của hình chóp tam giác đều là: \(\frac{{10.3}}{2}.12 = 180\) (\(c{m^2}\))
b) Diện tích xung quanh của hình chóp tứ giác đều là: \(\frac{{72.4}}{2}.77 = 11088\) (\(d{m^2}\))
Diện tích đáy của hình chóp tứ giác đều là: \({72^2}=5184\) (\(d{m^2}\))
Diện tích toàn phần của hình chóp tứ giác đều là: \(11088 + 5184 = 16 272\) (\(d{m^2}\))
Thể tích của hình chóp tứ giác đều là: \(\frac{1}{3}.5184.68,1=117676,8\) (\(d{m^3}\))
31 tháng 7 2023
Hình chóp tam giác đều nên là chiều cao của mặt bên xuất phát từ đỉnh chính là trung đoạn
Sxq=1/2*10*3*12=5*36=180cm2
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
a) Diện tích xung quanh của hình chóp tam giác đều là:
\(\frac{{99.40}}{2}.3 = 5940\) (\(c{m^2}\))
Diện tích đáy của hình chóp là:
\(\frac{{40.34,6}}{2} = 692\) (\(c{m^2}\))
Diện tích toàn phần của hình chóp là:
\(5940 + 692 = 6632\) (\(c{m^2}\))
Thể tích của hình chóp là:
\(\frac{1}{3}.692.98,3 \approx 22674,53\) (\(c{m^3}\))
b) Diện tích xung quanh của hình chóp tứ giác đều là:
\(\frac{{91.120}}{2}.4 = 21840\) (\(c{m^2}\))
Diện tích đáy của hình chóp là:
\(120.120 = 14400\) (\(c{m^2}\))
Diện tích toàn phần của hình chóp là:
\(21840 + 14400 = 36240\) (\(c{m^2}\))
Thể tích của hình chóp là:
\(\frac{1}{3}.14400.68,4 = 328320\) (\(c{m^3}\))
7 tháng 9 2023
a: Sxq=1/2*2,2*2,5*4=11m2
b: Diện tích cần làm mái che là: 11+2,5^2=17,25m2
Số tiền cần chi là:
17,25*2000000=34500000(đồng)
7 tháng 9 2023
Sxq=1/2*10*4*12=2*10*12=2*120=240cm2
Stp=240+10^2=340cm2
CM
3 tháng 3 2019
Đáp án A
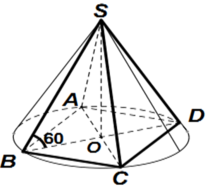
Gọi O là tâm của hình vuông ABCD.
Do S.ABCD là hình chóp đều nên SO ⊥ (ACBD)
Suy ra, OB là hình chiếu vuông góc của SB lên mp(ABCD)
Sxq=1/2*2,3*3*2,5=8,625cm2