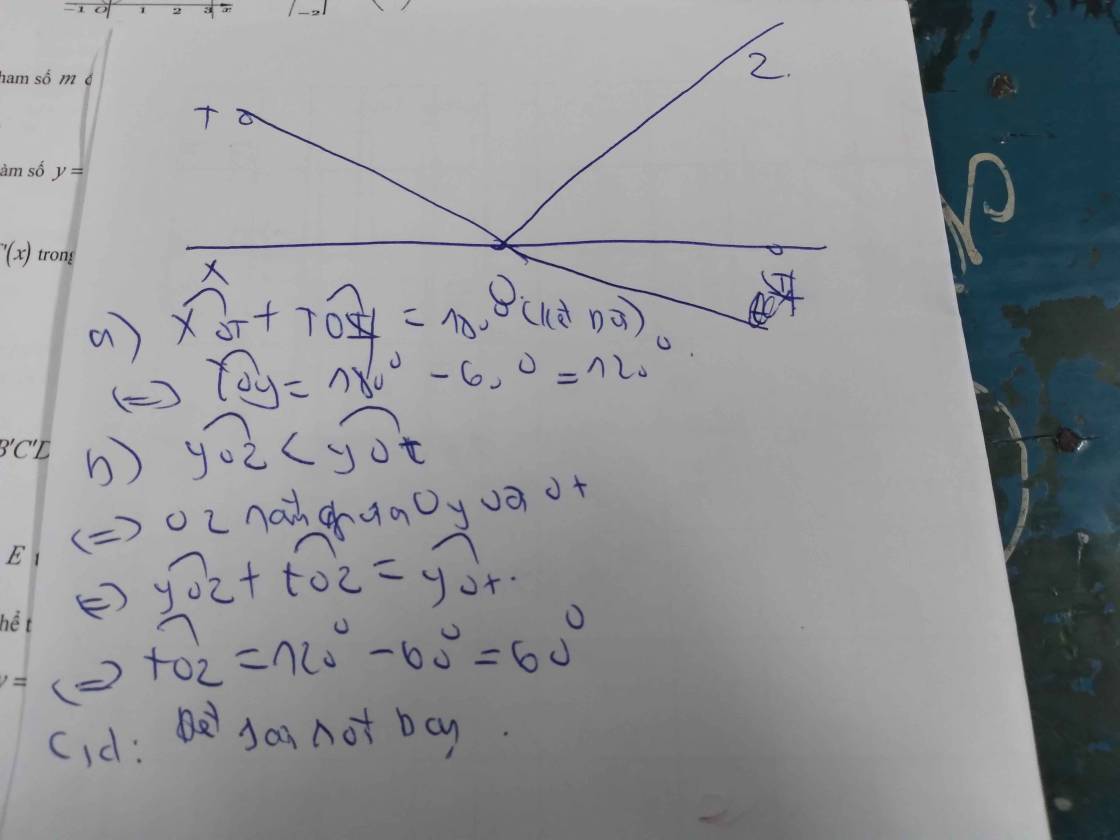
Trên đường thẳng XI lấy điểm O vẽ tia OT Sao chùa góc XÔT bằng 60° a) tính góc TÔY B) Trong góc TÔY vẽ tia OZ sao cho YOZ bằng 60°.Tính góc TÔZ C) vẽ tia Ôt là tia đối của tia Ôt so sánh ZÔy và YOt D)...

H

Hưng

6 tháng 9 2023

Trên đường thẳng XI lấy điểm O vẽ tia OT Sao chùa góc XÔT bằng 60° a) tính góc TÔY B) Trong góc TÔY vẽ tia OZ sao cho YOZ bằng 60°.Tính góc TÔZ C) vẽ tia Ôt là tia đối của tia Ôt so sánh ZÔy và YOt D) vẽ tia OZ là tia đối của tia Oz so sánh các góc xÔz ,ZÔt,xÔt vẽ hình...

Đọc tiếp

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

6 tháng 9 2023

loading...

Đúng(0)

TN

trương nguyễn hồng

19 tháng 6 2020 - olm

trên cùng một nữa mặt phẳng bờ chứa tia ox, xác định tia ot và oy sao cho góc xÔt = 25%, xooy = 50%. a) tia ôt có nằm giữa ox và oy không ? vì sao. b) so sánh hai góc xÔt và tÔy

#Toán lớp 6

0

HN

Hà Như Thuỷ

7 tháng 4 2016

Trên cùng một nửa mặt phẳng có bờ chứa tia Ox, vẽ hai tia Oy và Oz sao cho xÔy=60^o; xÔz=30^o. Biết zÔy=30^o và tia Oz là phân giác của xÔy. Gọi Ot là tia đối của tia Oz. Tính số đo góc tÔy.

Toán 6 nha

#Mẫu giáo

2

NP

Nguyễn Phương Anh

7 tháng 4 2016

Ta có: Ot và Oz là hai tia đối nhau=>tÔz là góc bẹt => tÔz=180*

=> Tia Oy nằm giữa hai tia Oz và Ot

=>tÔy+yÔz=tÔz

Thay số:tÔy+30*=180*

=>tÔy=180*-30*=150*

Vậy tÔy=150*

Đúng(0)

TM

Trần Minh Hoàng

27 tháng 7 2018

Do \(\widehat{xOz}< \widehat{xOy}\) và hai tia Oy và Oz cùng nằm trên một nửa mặt phẳng bờ chứa tia Ox nên Oz nằm giữa hai tia Oy và Ox.

Ot là tia đối của tia Oz \(\Rightarrow\) Hai góc tOy và yOz kề bù \(\Rightarrow\widehat{tOy}+\widehat{yOz}=180^o\)

\(\Rightarrow\widehat{tOy}+30^o=180^o\)

\(\Rightarrow\widehat{tOy}=180^o-30^o=150^o\)

Đúng(0)

DP

Duc Phan

28 tháng 4 2017 - olm

Trên cùng một nửa mặt phẳng bờ chứa tia Ox, vẽ 2 tia Ot và Oy sao cho xÔt = 30⁰và xOy = 70⁰,

a) Hỏi tia nào nằm giữa hai tia còn lại? vì sao ?

b) Tính tÔy. so sánh tÔy và xÔt

c)tia Ot có phải là tia phân giác của góc xÔy ko ? vì sao ?

d)Gọi Ot' là tia đối của tia Ot. Tính số đo góc của t'Ôy

Đây là câu thi hk2 của lớp 6 mn jup mình nha

#Toán lớp 6

2

Q

QuocDat

28 tháng 4 2017

a) => Vì \(\widehat{tOy}>\widehat{xOt}\) nên tia Ot là tia phân giác của \(\widehat{xOy}\)

b) \(\widehat{xOy}=\widehat{tOy}+\widehat{xOt}\)

\(70^o=\widehat{tOy}+30^o\)

\(\widehat{tOy}=70^o-30^o\)

\(\widehat{tOy}=40^o\)

Vì \(\widehat{tOy}=40^o\) và \(\widehat{xOt}=30^o\) nên \(\widehat{tOy}>\widehat{xOt}\left(40^o>30^o\right)\)

c) Tia Ot không phải là tia phân giác của \(\widehat{xOy}\) . Vì \(\widehat{xOt}\ne\widehat{tOy}\)

d) Vì Ot' là tia đối của Ot nên \(\Rightarrow\widehat{tOt'}=180^o\)

\(\widehat{tOt'}=\widehat{tOy}+\widehat{t'Oy}\)

\(180^o=70^o+\widehat{t'Oy}\)

\(\widehat{t'Oy}=180^o-70^o\)

\(\widehat{t'Oy}=110^o\)

Đúng(0)

DT

Dương Thị Huyền Thục

1 tháng 5 2017

Cho hai tia Oy, Oz nằm trên cùng một nửa mặt phẳng bờ chứa tia Ox sao cho xÔy = 75°; xÔz = 25°.

a) Trong ba tia Ox, Oy, Oz tia nào nằm giữa hai tia còn lại ?

b) Tính số đo yÔz

c) Gọi Om là tia phân giác của yÔz. Tính số đo xÔm.

Đúng(0)

HN

Huyền Nguyễn

6 tháng 7 2015 - olm

Cho điểm O nằm trên đường thẳng xy. Vẽ tia OZ sao cho góc xOz = 50 độ.

a, Tính góc yOz?

b, Vẽ tia Ot là tia đối của tia Oz. Tính góc yOt

Vẽ 2 tia Om, On lần lượt là tia phân giác của góc zOy và xOt. Vì sao Om là tia đối của tia on

#Toán lớp 6

1

NT

Nao Tomori

6 tháng 7 2015

dễ mà bạn, bạn xem lại lý thuyết đi là làm được , hoặc nhờ các bạn khác

Đúng(0)

NN

Nguyễn Ngọc Khánh

20 tháng 6 2015 - olm

cho 2 tia Ox và Oy đối nhau. Trên 2 nửa mặt phẳng bờ xy vẽ 2 tia Oz và Ot sao cho góc xOt = góc yOz= 40 độ

a, Tính góc yOt và so sánh góc yOt với xOz.

b, chứng minh tia Ot, Oz thẳng hàng

c, Vẽ tia Om là tia phân giác của góc tOy. Tính góc mOy

#Toán lớp 6

0

ZW

Za Warudo

8 tháng 7 2021

Cho góc bẹt xOy vẽ tia Oz sao cho yOz = 60 độ a) Tính góc zOx b)Trên nửa mặt phẳng Ox chứa Oz, vẽ tia Ot sao cho góc xOt = 60 độ.Chứng mình rằng Oz là tia phân giác của góc yOt c) Vẽ tia Om là tia phân giác của góc xOy.Hỏi hai góc zOm và góc mOt có phụ nhau ko,vì sao?

#Toán lớp 6

1

NL

Nguyễn Lê Phước Thịnh

8 tháng 7 2021

a) Ta có: \(\widehat{xOz}+\widehat{yOz}=180^0\)(hai góc kề bù)

\(\Leftrightarrow\widehat{yOz}+60^0=180^0\)

hay \(\widehat{yOz}=120^0\)

b) Ta có: \(\widehat{xOt}+\widehat{tOy}=180^0\)

\(\Leftrightarrow\widehat{tOy}+\dfrac{\widehat{xOz}}{2}=180^0\)

\(\Leftrightarrow\widehat{tOy}=120^0\)

Trên cùng một nửa mặt phẳng bờ chứa tia Oy, ta có: \(\widehat{yOz}< \widehat{yOt}\left(60^0< 120^0\right)\)

nên tia Oz nằm giữa hai tia Oy và Ot

mà \(\widehat{yOz}=\dfrac{1}{2}\widehat{yOt}\left(60^0=\dfrac{1}{2}\cdot120^0\right)\)

nên Oz là tia phân giác của \(\widehat{yOt}\)

Đúng(1)

ZW

Za Warudo

8 tháng 7 2021

Cho góc bẹt xOy vẽ tia Oz sao cho yOz = 60 độ a) Tính góc zOx b)Trên nửa mặt phẳng Ox chứa Oz, vẽ tia Ot sao cho góc xOt = 60 độ.Chứng mình rằng Oz là tia phân giác của góc yOt c) Vẽ tia Om là tia phân giác của góc xOy.Hỏi hai góc zOm và góc mOt có phụ nhau ko,vì sao?

#Toán lớp 6

1