Một khúc sông thẳng có vận tốc của dòng nước tăng tỉ lệ thuận với khoảng cách từ bờ. Vận tốc của dòng nước sát bờ là \(0\), ở giữa sông là \(v_0\). Một thuyền chạy băng qua dòng sông với tốc độ \(u\) không đổi và luôn vuông góc với vận tốc chảy của dòng nước. Cho sông có bề rộng \(c\). Xác định quãng đường thuyền bị nước cuốn đi khi đang ngang qua...
Đọc tiếp
Một khúc sông thẳng có vận tốc của dòng nước tăng tỉ lệ thuận với khoảng cách từ bờ. Vận tốc của dòng nước sát bờ là \(0\), ở giữa sông là \(v_0\). Một thuyền chạy băng qua dòng sông với tốc độ \(u\) không đổi và luôn vuông góc với vận tốc chảy của dòng nước. Cho sông có bề rộng \(c\). Xác định quãng đường thuyền bị nước cuốn đi khi đang ngang qua sông.
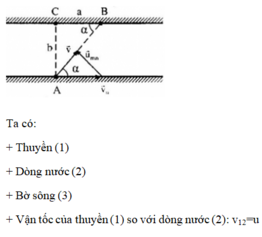
Để xác định quãng đường thuyền bị nước cuốn đi khi đang ngang qua sông, ta có thể sử dụng định luật Pythagoras và tỉ lệ của vận tốc dòng nước.
Gọi x là khoảng cách từ thuyền đến bờ sông. Vận tốc của dòng nước tại khoảng cách x từ bờ sông là v(x) = v0 + (v1 - v0) * (x / c), với v1 là vận tốc của dòng nước tại bờ sông và c là bề rộng của sông.
Vận tốc của thuyền là u, luôn vuông góc với vận tốc chảy của dòng nước. Do đó, vận tốc tương đối của thuyền so với dòng nước là v(x) - u.
Áp dụng định luật Pythagoras, ta có: (v(x) - u)^2 = v0^2 + u^2
Giải phương trình trên để tìm x, ta có: (v0 + (v1 - v0) * (x / c) - u)^2 = v0^2 + u^2 (v1 - v0) * (x / c) = sqrt(v0^2 + u^2) - v0 x = (sqrt(v0^2 + u^2) - v0) * (c / (v1 - v0))