Một quả bóng bida khối lượng 0,35 kg va chạm vuông góc vào mặt bên của mặt bida và bật ra cũng vuông góc. Tốc độ của nó trước khi va chạm là 2,8 m/s và tốc độ sau khi va chạm là 2,5 m/s. Tính độ thay đổi động lượng của quả bida.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn chiều dương là chiều chuyển động của quả cầu đập vào tường
Động lượng của quả cầu trước va chạm: p = m.v = 2.3,0 = 6,0 (kg.m/s)
Động lượng của quả cầu sau va chạm: p’ = -m.v’ = -2,3,0 = -6,0 (kg.m/s)
=> Động lượng của quả cầu sau va chạm giảm
Động năng của quả cầu trước va chạm là: \({W_d} = \frac{1}{2}m{v^2} = \frac{1}{2}.2.{(3,0)^2} = 9,0(J)\)
Động năng của quả cầu sau va chạm là: \(W_d^; = \frac{1}{2}mv{'^2} = \frac{1}{2}.2.{( - 3,0)^2} = 9,0(J)\)
=> Động năng không thay đổi

Chọn C.
+ Biểu diễn véc tơ động lượng lúc trước và lúc sau
+ p → động lượng lúc trước.
+ p ' → động lượng lúc sau.
+ Độ biến thiên động lượng của quả bóng do va chạm
![]()
+ Từ hình biểu diễn véc tơ ta có độ lớn:
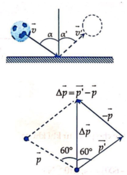
∆p = p’ = p = m.v = 0,2.25 = 5 kg.m/s.
(vì tam giác tạo bởi 3 cạnh này là tam giác cân có 1 góc 60° là tam giác đều).

Chọn C.
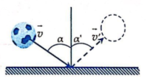
+ Biểu diễn véc tơ động lượng lúc trước và lúc sau
+ p ⇀ động lượng lúc trước.
+ p ' ⇀ động lượng lúc sau.
+ Độ biến thiên động lượng của quả bóng do va chạm
δ p ⇀ = p ' ⇀ - p ⇀ = p ' ⇀ + - p ⇀
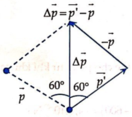
+ Từ hình biểu diễn véc tơ ta có độ lớn:
∆ p = p’ = p = m.v = 0,2.25 = 5 kg.m/s.
(vì tam giác tạo bởi 3 cạnh này là tam giác cân có 1 góc 60° là tam giác đều).

Chọn chiều chuyển động ban đầu của quả cầu A là chiều dương. Hệ vật gồm hai quả cầu A và B. Gọi v 1 , v 2 và v ' 1 , v ' 2 là vận tốc của hai quả cầu trước và sau khi va chạm.
Vì hệ vật chuyển động không ma sát và ngoại lực tác dụng lên hệ vật (gồm trọng lực và phản lực của máng ngang) đều cân bằng nhau theo phương thẳng đứng, nên tổng động lượng của hệ vật theo phương ngang được bảo toàn (viết theo trị đại số):
m 1 v ' 1 + m 2 v ' 2 = m 1 v 1 + m 2 v 2
2. v ' 1 + 3. v ' 2 = 2.3 +3.1 = 9
Hay v ' 1 + 1,5. v ' 2 = 4,5 ⇒ v ' 2 = 3 - 2 v ' 1 /3 (1)
Đồng thời, tổng động năng của hệ vật cũng bảo toàn, nên ta có:
m1 v ' 1 2 /2 + m2 v ' 2 2 /2 = m1 v 1 2 /2 + m2 v 2 2 /2
2 v ' 1 2 /2 + 3 v ' 2 2 /2 = 2. 3 2 /2 + 3. 1 2 /2
Hay v ' 1 2 + 1,5 v ' 2 2 = 10,5 ⇒ v ' 2 2 = 7 - 2 v ' 1 2 /3 (2)
Giải hệ phương trình (1), (2), ta tìm được: v ' 1 = 0,6 m/s; v ' 2 = 2,6 m/s
(Chú ý: Loại bỏ cặp nghiệm v ' 1 = 3 m/s, v ' 2 = 1 m/s, vì không thỏa mãn điều kiện v ' 2 > v 2 = 1 m/s)

Chon chiều dương như hình vẽ theo bài ra
v 1 = v 2 = v = 10 ( m / s )
Độ biến thiên động lượng
Δ p → = p → 2 − p → 1 = m v → 2 − m v → 1
Chiếu lên chiều dương
⇒ Δ p = − m v 2 sin α − m v 1 sin α = − 2 m v sin α
Lực trung bình do sàn tác dụng lên bóng
Δ p = F . Δ t ⇒ F = Δ p Δ t
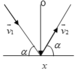
a. với α = 30 0
Ta có Δ p = − 2 m v sin α = − 2.0 , 5.10. sin 30 0 = − 5 ( k g m / s )
Lực trung bình do sàn tác dụng lên bóng
F = Δ p Δ t = − 5 0 , 1 = − 50 ( N )
b. Với α = 90 0
Ta có Δ p = − 2 m v sin α = − 2.0 , 5.10. sin 90 0 = − 10 ( k g m / s )
Lực trung bình do sàn tác dụng lên bóng
F = Δ p Δ t = − 10 0 , 1 = − 100 ( N )

Giải thích: Đáp án D
Phương pháp :
- Áp dụng định luật bảo toàn động lượng và định luật bảo toàn động năng
- Sử dung̣ hê ̣thức đôc̣ lâp̣ với thời gian của li đô ̣vàvâṇ tốc
Biên độ dao động ban đầu: ![]()
Cách giải:
Hai vật va chạm đàn hồi xuyên tâm nên áp dụng ĐL bảo toàn động lượng và động năng ta được:
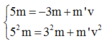
Giải hệ ta được v = 2cm/s
Áp dụng hệ thức độ lập: 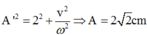
Vậy quãng đường đi được sau va chạm đến khi đổi chiều chuyển động là

Chọn A.
Chọn chiều dương là chiều chuyển động của quả bóng sau khi va chạm.
Lực của tường tác dụng lên quả bóng:
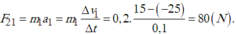

Độ thay đổi động lượng của quả bida là:
\(\Delta p = \left| {{p_s} - {p_{tr}}} \right| = \left| {m.{v_s} - m.{v_{tr}}} \right| = \left| {0,25(2,5 - 2,8)} \right| = 0,075(kg.m/s)\)