giá trị của f(9) biết hàm số f(x)=12/x
Làm nhanh mk tick
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PP
1
8 tháng 2 2020
Ta có: \(f\left(x\right)=-2x+1\)
\(\Rightarrow\hept{\begin{cases}f\left(1-2x\right)=-2\left(1-2x\right)+1=4x-1\\f\left(2-x\right)=-2\left(2-x\right)+1=2x-3\end{cases}}\)
Vì \(f\left(1-2x\right)=f\left(2-x\right)\Rightarrow f\left(1-2x\right)-f\left(2-x\right)=0\)
Để \(f\left(1-2x\right)-f\left(2-x\right)=0\Rightarrow4x-1-\left(2x-3\right)=0\)
\(\Rightarrow4x-1-2x+3=0\Rightarrow2x+2=0\Rightarrow2\left(x+1\right)=0\)
\(\Rightarrow x+1=\frac{0}{2}=0\Rightarrow x=0-1\Rightarrow x=-1\)
MT
0
CM
4 tháng 6 2017
Chọn B
Từ đồ thị của hàm số f'(x) trên đoạn [0;4] ta có bảng biến thiên của hàm số trên đoạn [0;4] như sau:
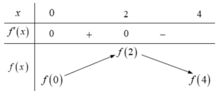
Từ bảng biến thiên ta có 
Mặt khác 
Suy ra 
16 tháng 12 2020
a, f (-1)= 5 - 3.(-1)= 8
f (0) = 5 - 3. 0= 5
|
c, bn lm đi nhá, mà câu b lỗi xin lỗi nhé
CM
9 tháng 9 2018
Chọn A
Từ đồ thị của hàm số y = f'(x) ta có bảng biến thiên của hàm số y = f(x) trên đoạn [-1;2] như sau
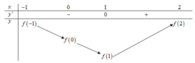
Nhận thấy
Để tìm 
ta so sánh f(-1) và f(2)
Theo giả thiết, 
Từ bảng biến thiên , ta có f(0) - f(1) > 0. Do đó f(2) - f(-1) > 0 
HN
1
21 tháng 10 2021
\(f\left(6\right)-f\left(2\right)=12\)
\(\Leftrightarrow6a+b-2a-b=12\)
\(\Leftrightarrow a=3\)
=> f(x)=3x+b
\(f\left(12\right)-f\left(2\right)=36+b-6-b=30\)
9 tháng 12 2020
y = f(x) = -4x + 1
a) y = f(-1) = -4.(-1) + 1 = 5
y = f(1/2) = -4.1/2 + 1 = -1
b) Để y = 0 <=> -4x + 1 = 0 <=> x = 1/4
Để y = -3 <=> -4x + 1 = -3 <=> x = 1
f(9)=12/9
<=>f(9)=\(\frac{3.4}{3.3}\)=\(\frac{3}{4}\)
k mk nha