Cho góc xoy=120°.Vẽ Tia oz là phân giác.
A) Tính góc xoz
B)trên tia oz lấy điểm A.Từ A vẽ tia AB,B thuộc tia Oy sao cho OAB=60°.Chứng Minh AB song song với ox.
C)Vẽ Tia AT sao cho Bat=90°.Chứng minh AT vuông góc với ox
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 1 2022
a: Xét ΔADO và ΔBDO có
OA=OB
\(\widehat{AOD}=\widehat{BOD}\)
OD chung
Do đó: ΔADO=ΔBDO
b: Xét ΔOED vuông tại E và ΔOFD vuông tại F có
OD chung
\(\widehat{EOD}=\widehat{FOD}\)
Do đó: ΔOED=ΔOFD
Suy ra: OE=OF
c: Xét ΔOAB có
OE/OA=OF/OB
Do đó: EF//AB
9 tháng 12 2023
a: Xét ΔOAI và ΔOBI có
OA=OB
\(\widehat{AOI}=\widehat{BOI}\)
OI chung
Do đó: ΔOAI=ΔOBI
b: Ta có: ΔOAI=ΔOBI
=>IA=IB
=>I nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OI là đường trung trực của BA
=>OI\(\perp\)AB
=>Oz\(\perp\)AB
c: ta có: Oz\(\perp\)AB
AB//CD
Do đó: Oz\(\perp\)CD tại I
Xét ΔOCD có
OI là đường cao
OI là đường phân giác
Do đó;ΔOCD cân tại O
Ta có: ΔOCD cân tại O
mà OI là đường cao
nên I là trung điểm của CD
d: Ta có: OB+BD=OD
OA+AC=OC
mà OB=OA
và OC=OD
nên BD=AC
Xét ΔBDC và ΔACD có
BD=AC
\(\widehat{BDC}=\widehat{ACD}\)(ΔOCD cân tại O)
CD chung
Do đó: ΔBDC=ΔACD
=>\(\widehat{BCD}=\widehat{ADC}\)
=>\(\widehat{MCD}=\widehat{MDC}\)
Xét ΔMCD có \(\widehat{MCD}=\widehat{MDC}\)
nên ΔMCD cân tại M
=>MC=MD
=>M nằm trên đường trung trực của CD(3)
Ta có: ΔOCD cân tại O
mà OI là đường cao
nên OI là đường trung trực của CD(4)
Từ (3) và (4) suy ra O,M,I thẳng hàng
CM
28 tháng 9 2018
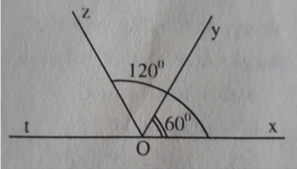
a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox có hai tia Oy, Oz và x O y ^ < x O z ^ ( vì 60 ° < 120 ° ) nên tia Oy nằm giữa hai tia Ox, Oz
Ta có:
x O y ^ + y O z ^ = x O z ^
60 ° + y O z ^ = 120 °
y O z ^ = 120 ° - 60 ° = 60 °
Tia Oy nằm giữa hai tia Ox, Oz và x O y ^ = y O z ^ ( = 60 ° )
Vậy tia Oy là phân giác của góc xOz
b) Hai góc xOz và zOt kề bù , nên: x O z ^ + z O t ^ = 180 °
120 ° + z O t ^ = 180 °
z O t ^ = 180 ° - 120 ° = 60 °
Tia Oz nằm giữa hai tia Oy, Ot và y O z ^ = z O t ^ ( = 60 ° )
Vậy tia Oz là phân giác của góc yOt
LV
26 tháng 10 2017
a) Ta có \(\widehat{xOz}=\widehat{zOy}=\frac{1}{2}\widehat{xOy}=\frac{120^0}{2}=60^0\)
MÀ Oz // At
=> \(\widehat{zOy}=\widehat{tAy}=60^0\)
VẬY \(\widehat{tAy}=60^0\)
b) Vì Am // Ox
=>\(\widehat{xOy}=\widehat{mAy}=120^0\)
MÀ \(\widehat{mAt}+\widehat{tAy}=\widehat{mAY}\)
=> \(\widehat{mAt}=60^0\)
=> \(\widehat{mAt}=\frac{1}{2}\widehat{xOy}\)
HAY \(\widehat{mAt}< \widehat{xOy}\)(đpcm)
ĐÚNG HAY SAI THÌ MK CKIU