Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) Hai góc ∠xOz và ∠zOt kề bù , nên: ∠xOz + ∠zOt = 180 0
120 0 + ∠zOt = 180 0
∠zOt = 180 0 - 120 0 = 60 0
Tia Oz nằm giữa hai tia Oy, Ot và ∠yOz = ∠zOt ( = 60 0 )
Vậy tia Oz là phân giác của góc ∠yOt

a) Xét 3 góc\(yOz+zOx+xOy\) = 360 độ (định lí) .Mà \(xOy\) và \(xOz\) đều bằng 120 độ (gt)
\(\Rightarrow yOz=360^0-xOz-xOy=360^0-120^0-120^0=120^0\)
Mà góc \(xOy\) , \(xOz\) cũng bằng \(120^0\) nên 3 góc đó bằng nhau hay góc \(xOy=xOz=yOz\Rightarrow\left(đcpm\right)\)
b) Do Oa là tia đối tia \(Ox\)nên góc aOx bằng \(180^0\)
Ta có : góc O1 + góc yOx = aOx (Oy nằm giữa Oa và Ox)
Mà góc \(yOx\) bằng \(120^0\) => góc O1 = \(180^0-120^0=60^0\) \(=\frac{1}{2}=120^0\)
Ta thấy: \(yOz=120^0\Rightarrow\) Oa là tia p/g góc yOz NOTE
...

x' x z' y z
a) Ta có: \(\widehat{x'Oy}=4\widehat{xOz}\)
\(\Rightarrow\widehat{x'Oy}=4.30^o=120^o\)
Lại có: \(\widehat{zOy}=180^o-\widehat{xOz'}-\widehat{yOx'}\)
hay \(\widehat{zOy}=180^o-30^o-120^o\)
\(\widehat{zOy}=30^o\)
\(\Rightarrow\widehat{xOz}=\widehat{zOy}\left(=30^o\right)\)
mà Oz nằm giữa góc xOy
oz là tia phân giác của góc xoy.
b) Ta có: \(\widehat{yOz'}=\frac{120^o}{2}\)( vì oz' là tia phân giác của góc x'oy)
\(\Rightarrow\widehat{yOz'}=60^o\)
\(\Rightarrow\widehat{zOz}=\widehat{zOy}+\widehat{yOz'}\)
\(\Rightarrow\widehat{zOz'}=30^o+60^o\)
\(\Rightarrow\widehat{zOz'}=90^o\)
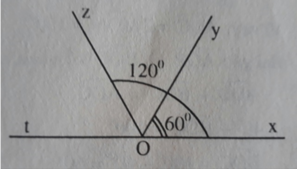
a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox có hai tia Oy, Oz và x O y ^ < x O z ^ ( vì 60 ° < 120 ° ) nên tia Oy nằm giữa hai tia Ox, Oz
Ta có:
x O y ^ + y O z ^ = x O z ^
60 ° + y O z ^ = 120 °
y O z ^ = 120 ° - 60 ° = 60 °
Tia Oy nằm giữa hai tia Ox, Oz và x O y ^ = y O z ^ ( = 60 ° )
Vậy tia Oy là phân giác của góc xOz
b) Hai góc xOz và zOt kề bù , nên: x O z ^ + z O t ^ = 180 °
120 ° + z O t ^ = 180 °
z O t ^ = 180 ° - 120 ° = 60 °
Tia Oz nằm giữa hai tia Oy, Ot và y O z ^ = z O t ^ ( = 60 ° )
Vậy tia Oz là phân giác của góc yOt