
cho tôi xin đáp án nhanh nhất có thể nha
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(16x^2-1\)
\(=\left(4x\right)^2-1^2\)
\(=\left(4x-1\right)\left(4x+1\right)\)
b) \(\left(x+2\right)^2-49y^2\)
\(=\left(x+2\right)^{^2}-\left(7y\right)^2\)
\(=\left[\left(x+2\right)-7y\right]\left[\left(x+2\right)+7y\right]\)
\(=\left(x+2-7y\right)\left(x+2+7y\right)\)
c) \(4x^2-12xy+9y^2\)
\(=\left(2x\right)^2-2\cdot2x\cdot3y+\left(3y\right)^2\)
\(=\left(2x-3y\right)^2\)
d) \(\left(a+b\right)^2-\left(2a-b\right)^2\)
\(=\left[\left(a+b\right)+\left(2a-b\right)\right]\left[\left(a+b\right)-\left(2a-b\right)\right]\)
\(=\left(a+b+2a-b\right)\left(a+b-2a+b\right)\)
\(=3a\cdot\left(2b-a\right)\)
e) \(\left(x-y\right)^2-2\left(x-y\right)z+z^2\)
\(=\left[\left(x-y\right)-z\right]^2\)
\(=\left(x-y-z\right)^2\)
g) \(-3x^2+6xy-3y^2\)
\(=-\left(3x^2-6xy+3y^2\right)\)
\(=-3\left(x^2-2xy+y^2\right)\)
\(=-3\left(x-y\right)^2\)
a: 16x^2-1=(4x)^2-1=(4x-1)(4x+1)
b: (x+2)^2-49y^2
=(x+2)^2-(7y)^2
=(x+2+7y)(x+2-7y)
c: 4x^2-12xy+9y^2=(2x-3y)^2
d: (a+b)^2-(2a-b)^2
=(a+b+2a-b)(a+b-2a+b)
=(2b-a)*3a
g: =-3(x^2-2xy+y^2)
=-3(x-y)^2

\(a,6a^2b+9ab^2\)
\(=3ab\left(2a+3b\right)\)
\(b,5x^3y^2-15x^2y^3\)
\(=5x^2y^2\left(x-3y\right)\)
\(c,2x\left(x+1\right)-3y\left(x+1\right)\)
\(=\left(x+1\right)\left(2x-3y\right)\)
\(d,\left(x-y\right)^2-x\left(x-y\right)\)
\(=\left(x-y\right)\left(x-y-x\right)\)
\(=-y\left(x-y\right)\)
\(e,y\left(x-1\right)-x\left(1-x\right)\)
\(=y\left(x-1\right)+x\left(x-1\right)\)
\(=\left(x-1\right)\left(y+x\right)\)
\(g,2a\left(a-b\right)+2b\left(b-a\right)\)
\(=2a\left(a-b\right)-2b\left(a-b\right)\)
\(=\left(2a-2b\right)\left(a-b\right)\)
\(=2\left(a-b\right)^2\)
#Urushi☕
a: 6a^2b+9ab^2
=3ab*2a+3ab*3b
=3ab(2a+3b)
b: 5x^3y^2-15x^2y^3
=5x^2y^2*x-5x^2y^2*3y
=5x^2y^2(x-3y)
c: 2x(x+1)-3y(x+1)
=(x+1)(2x-3y)
d: =(x-y)(x-y-x)
=-y(x-y)
e: =y(x-1)+x(x-1)
=(x-1)(x+y)
g: =2a(a-b)-2b(a-b)
=(a-b)(2a-2b)
=2(a-b)^2

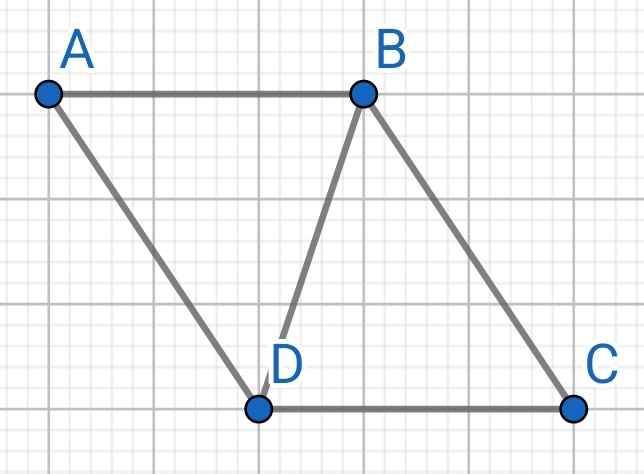 Do AB // CD (gt)
Do AB // CD (gt)
⇒ ∠ABD = ∠CDB (so le trong)
Xét ∆ABD và ∆CDB có:
AB = CD (gt)
∠ABD = ∠CDB (cmt)
BD chung
⇒ ∆ABD = ∆CDB (c-g-c)
⇒ AD = BC (hai cạnh tương ứng)
Do ∆ABD = ∆CDB (cmt)
⇒ ∠ADB = ∠CBD (hai góc tương ứng)
Mà ∠ADB và ∠CBD là hai góc so le trong
⇒ AD // BC

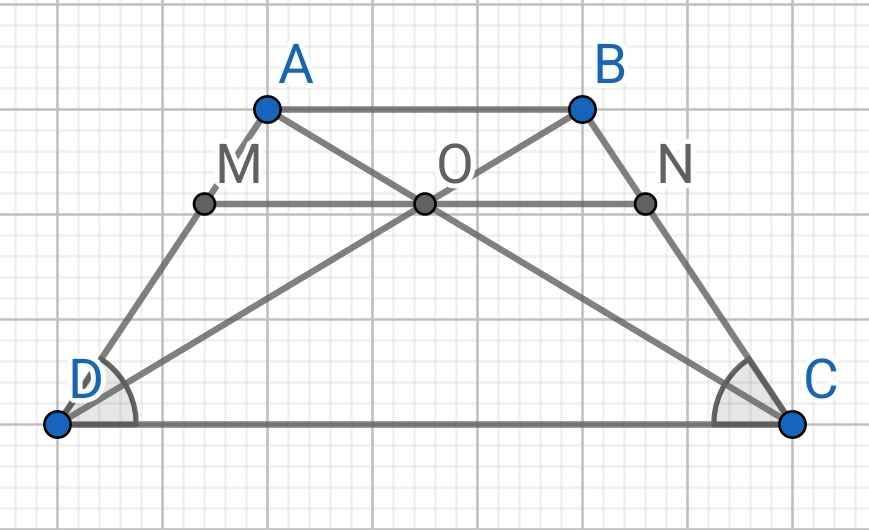 a) Do ABCD là hình thang cân
a) Do ABCD là hình thang cân
⇒ AD = BC (hai cạnh bên)
∠ADC = ∠BCD (hai góc kề đáy CD)
Xét ∆ADC và ∆BCD có:
AD = BC (cmt)
∠ADC = ∠BCD (cmt)
CD chung
⇒ ∆ADC = ∆BCD (c-g-c)
⇒ ∠ACD = ∠BDC (hai góc tương ứng)
b) Do MN // AB // CD
⇒ ON // AB // CD
Do CD // ON (cmt)
⇒ ∠ACD = ∠NOC (so le trong)
Do CD // AB (gt)
⇒ ∠BDC = ∠ABD (so le trong)
Do AB // ON (cmt)
⇒ ∠ABD = ∠BON (so le trong)
c) Do ∠ACD = ∠NOC (cmt)
∠ACD = ∠BDC (cmt)
⇒ ∠NOC = ∠BDC
Mà ∠BDC = ∠ABD (cmt)
⇒ ∠NOC = ∠ABD
Lại có ∠ABD = ∠BON (cmt)
⇒ ∠NOC = ∠BON
Vậy ON là tia phân giác của ∠BOC



4 tấn 25 kg = 4025 kg
kho thứ nhất
\(4025:\left(2+3\right)\times2=1610\left(kg\right)\)
kho thứ hai
\(4020-1610=2415\left(kg\right)\)
$#flo2k9$
đổi `4 tấn 25 kg = 2025 kg`
kho thứ nhất có : `4025 : ( 2 +3 ) xx 2 = 1610(kg)`
kho thứ 2 có : `4025 - 1610 = 2415(kg)`

8-4 : 3/4 =8-13/4
3/7:3/5 -4/7 =5/7-4/7=1/7
5/8 x 2/5 + 5/8 x3/5 =5/8 x (2/5+3/5)=5/8 x 1=5/8
$#flo2k9$
`8 - 4 : 3/4 = 8 - 4 xx 4/3 = 8 - 16/3 = 8/3`
`3/7 : 3/5 - 4/7 = 3/7 xx 5/3 - 4/7 = 5/7 - 4/7 = 1/7`
`5/8 xx 2/5 + 5/8 xx 3/5 = 5/8 xx ( 2/5 + 3/5) = 5/8 xx 1= 5/8`
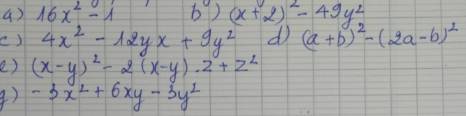



1: Xét tứ giác ABEC có
AB//EC
AC//BE
=>ABEC là hình bình hành
=>BE=AC
mà AC=BD
nên BE=BD
2:
ΔBED cân tại B
mà BH là đường cao
nên H là trung điểm của DE
3: Xét ΔABC và ΔBAD có
BA chung
BC=AD
AC=BD
Do đó: ΔABC=ΔBAD
=>góc OAB=góc OBA
=>OA=OB
OA+OC=AC
OB+OD=BD
mà OA=OB và AC=BD
nên OC=OD