Cho tam giác ABC vuông tại A có AB < AC Vẽ AH vuông góc với BC trên tia đối của ha lấy điểm D sao cho HD = ha Trên tia bc lấy điểm K sao cho HK = HB
a. Chứng minh Tam giác AHK=DHP
b.AK song song với BD
c.AB =BD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔBHA vuông tại H và ΔBHD vuông tại H có
BH chung
AH=DH(gt)
Do đó: ΔBHA=ΔBHD(hai cạnh góc vuông)
b) Xét ΔHBA vuông tại H và ΔHKD vuông tại H có
HB=HK(gt)
HA=HD(gt)
Do đó: ΔHBA=ΔHKD(hai cạnh góc vuông)
⇒\(\widehat{HBA}=\widehat{HKD}\)(hai góc tương ứng)
mà \(\widehat{HBA}\) và \(\widehat{HKD}\) là hai góc ở vị trí so le trong
nên AB//DK(Dấu hiệu nhận biết hai đường thắng song song)
c) Ta có: AB//DK(cmt)
AB⊥AC(ΔABC vuông tại A)
Do đó: DK⊥AC
Xét ΔDAK có
KH là đường cao ứng với cạnh AD(KH⊥AD)
AC là đường cao ứng với cạnh DK(AC⊥DK)
KH\(\cap\)AC={C}
Do đó: C là trực tâm của ΔDAK(Tính chất ba đường cao của tam giác)
⇒DC⊥AK(đpcm)

a: Xét ΔABH vuông tại H và ΔKIH vuông tại H có
HA=HK
HB=HI
=>ΔABH=ΔKIH
b: ΔABH=ΔKIH
=>góc ABH=góc KIH
=>AB//IK
c: IK//AB
AB vuông góc AC
=>IK vuông góc AC
=>I,K,E thẳng hàng
d: Xét tứ giác ABKI có
H là trung điểm chung của AK và BI
AK vuông góc BI
=>ABKI là hình thoi
=>AB=AI=IK
=>IK=ID
=>góc IKD=góc IDK

a: Đặt AB/3=AC/4=k
=>AB=3k; AC=4k
Xét ΔBAC vuông tại A có \(AB^2+AC^2=BC^2\)
\(\Leftrightarrow25k^2=100\)
=>k=2
=>AB=6cm; AC=8cm
b: Xét ΔCAD có
CH là đường cao
CH là đường trung tuyến
Do đo: ΔCAD cân tại C
hay CA=CD
Xét ΔBAD có
BH là đườg cao
BH là đường trung tuyến
Do đo:ΔBAD cân tại B
Xét ΔCAB và ΔCDB có
CA=CD
AB=DB
CB chung
Do đó: ΔCAB=ΔCDB
Suy ra: \(\widehat{CAB}=\widehat{CDB}=90^0\)
hay ΔBDC vuông tại D
c: Xét ΔDAE có
C là trung điểm của DE
H là trung điểm của DA
DO đó:CH là đường trung bình
=>CH//AE
hay AE//BC

a: Đặt AB/3=AC/4=k
=>AB=3k; AC=4k
Xét ΔBAC vuông tại A có \(AB^2+AC^2=BC^2\)
\(\Leftrightarrow25k^2=100\)
=>k=2
=>AB=6cm; AC=8cm
b: Xét ΔCAD có
CH là đường cao
CH là đường trung tuyến
Do đo: ΔCAD cân tại C
hay CA=CD
Xét ΔBAD có
BH là đườg cao
BH là đường trung tuyến
Do đo:ΔBAD cân tại B
Xét ΔCAB và ΔCDB có
CA=CD
AB=DB
CB chung
Do đó: ΔCAB=ΔCDB
Suy ra: \(\widehat{CAB}=\widehat{CDB}=90^0\)
hay ΔBDC vuông tại D
c: Xét ΔDAE có
C là trung điểm của DE
H là trung điểm của DA
DO đó:CH là đường trung bình
=>CH//AE
hay AE//BC

xét tam giác ABE và tam giác ADE
AE chung
góc BAE = góc DAE(AE la tia phân giác của góc E)
AB = AD ( gt)
=> tam giác ABE = tam giac DAE ( c.g.c)
b) xét tam giác ABI và tam giác ADI
AI chung
góc BAE = góc DAE
tam giác ABI=tam giác ADI
=> BI = DI ( 2 cạnh t/ứ )
=> I là trung điểm của BD

\(\text{#TNam}\)
`a,` Xét Tam giác `AMB` và Tam giác `EMC` có:
`MA=ME (g``t)`
\(\widehat{AMB}=\widehat{CME} (\text {2 góc đối đỉnh})\)
`MB=MC (\text {M là trung điểm của BC})`
`=> \text {Tam giác AMB = Tam giác EMC (c-g-c)}`
`b,` Vì Tam giác `AMB =` Tam giác `EMC (a)`
`-> AB = CE (\text {2 cạnh tương ứng}) (1)`
Xét Tam giác `ABH` và Tam giác `DBH` có:
`HA = HD (g``t)`
\(\widehat{AHB}=\widehat{DHB}=90^0\)
`\text {BH chung}`
`=> \text {Tam giác ABH = Tam giác DBH (c-g-c)}`
`-> AB = BD (\text {2 cạnh tương ứng}) (2)`
Từ `(1)` và `(2) -> CE = BD.`
`c,` Xét Tam giác `AMH` và Tam giác `DMH` có:
`\text {MH chung}`
\(\widehat{AHM}=\widehat{DHM}=90^0\)
`HA = HD (g``t)`
`=> \text {Tam giác AMH = Tam giác DMH (c-g-c)}`
`-> MA = MD (\text {2 cạnh tương ứng})`
Xét Tam giác `AMD: MA = MD`
`-> \text {Tam giác AMD cân tại M}`
*Hoặc nếu như bạn có học rồi, thì mình có thể dùng cái này cũng được nè cậu:>.
Vì `MH` vừa là đường cao (hạ từ đỉnh `->` cạnh đối diện), vừa là đường trung tuyến.
Theo tính chất của tam giác cân `-> \text {Tam giác AMD là tam giác cân} (đpcm).`
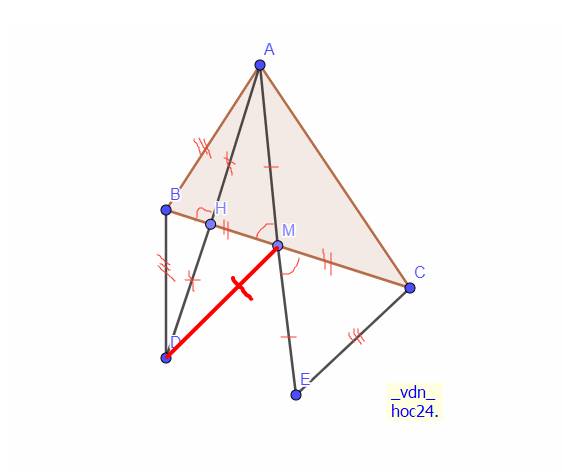
a: Xét ΔAMB và ΔEMC có
MA=ME
góc AMB=góc EMC
MB=MC
=>ΔAMB=ΔEMC
b: Xét ΔBAD có
BH vừa là đường cao, vừa là trung tuyến
=>ΔBAD cân tại B
=>BD=BA=CE
c: Xét ΔMAD có
MH vừa là đường cao, vừa là trung tuyến
=>ΔMAD cân tại M
b: Xét tứ giác ABDK có
H là trung điểm chung của AD và BK
AD vuông góc BK tại H
Do đó: ABDK là hình thoi
=>AK//BD
c: ABDK là hình thoi
=>AB=BD
Câu a đâu bạn