Cho hai biến cố xung khắc \(A\) và \(B\). Có 5 kết quả thuận lợi cho biến cố \(A\) và 12 kết quả thuận lợi cho biến cố \(B\). Hãy so sánh \(P\left( {A \cup B} \right)\) với \(P\left( A \right) + P\left( B \right)\).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
1 tháng 10 2023
Các kết quả thuận lợi cho biến cố A là A = {Hương; Hồng; Dung}.
Các kết quả thuận lợi cho biến cố B là B = { Hương; Hồng; Hoàng}.
22 tháng 8 2023
tham khảo
a)\(P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)-P\left(AB\right).\)
Suy ra \(P\left(AB\right)=0,4\)
\(P\left(\overline{A}B\right)=P\left(B\right)-P\left(AB\right)=0,7-0,4=0,3\)
\(P\left(\overline{A}\overline{B}\right)=1-P\left(A\cup B\right)=0,2\)
b) Vì \(P\left(AB\right)\ne P\left(A\right).P\left(B\right)\) nên A và B không độc lập.
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
a) \(A\) và \(B\) là hai biến cố độc lập \( \Rightarrow P\left( {AB} \right) = P\left( A \right)P\left( B \right) \Rightarrow P\left( B \right) = \frac{{P\left( {AB} \right)}}{{P\left( A \right)}} = \frac{2}{3}\)
\( \Rightarrow P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = \frac{{23}}{{30}}\)
b) \(A\) và \(B\) là hai biến cố độc lập \( \Rightarrow P\left( {AB} \right) = P\left( A \right)P\left( B \right) = 0,5.P\left( A \right)\)
\(\begin{array}{l}P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) \Leftrightarrow 0,7 = P\left( A \right) + 0,5 - 0,5.P\left( A \right)\\ \Leftrightarrow 0,5P\left( A \right) = 0,2 \Leftrightarrow P\left( A \right) = 0,4\end{array}\)
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
a) Số nguyên dương nhỏ hơn 100 luôn có 1 hoặc 2 chữ số nên ta có không gian mẫu của phép thử trên là: \(\Omega = \left\{ {1,2,3,4,5,...98,99} \right\}\)
b) Tập hợp biến cố A: “Số được chọn là số chính phương” là:
\(A = \left\{ {{a^2}\left| {a = 1,2,...,9} \right.} \right\}\)
c) Cứ 4 số thì có 1 số chia hết cho 4, số nhỏ nhất là 4 và lớn nhất là 96 nên số kết quả thuận lợi cho biến cố B là \(\dfrac{96-4}{4}+1=24\).
Vậy có 24 kết quả thuận lợi cho biến cố B: “Số được chọn chia hết cho 4”
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
27 tháng 9 2023
\(a,\Omega=\left\{1;2;3;4;5;...;98;99\right\}\\ b,A=\left\{1;4;9;16;25;36;49;64;81\right\}\\c, B=\left\{4;8;16;20;24;...;92;96\right\}\\ Số.kết.quả.thuận.lợi.cho.B:\left(96-4\right):4+1=24\left(kết.quả\right)\)
HQ
Hà Quang Minh
Giáo viên
11 tháng 1
a) Có 2 khả năng có thể xảy ra đối với mặt xuất hiện của đồng xu là: Sấp (S) và Ngửa (N).
Vậy \(A = \left\{ {S;\,N} \right\}\).
b) Biến cố B: “Mặt xuất hiện của đồng xu là mặt N”
Tập hợp M gồm các kết quả xó thể xảy ra đối với biến cố B là: \(M = \left\{ N \right\}\).
Phần tử N là kết quả thuận lợi cho biến cố B.
c) Số các kết quả thuận lợi của B là: 1
Số phần tử của tập hợp A là: 2
Tỉ số các kết quả thuận lợi cho biến cố B và phần tử của tập hợp A là: \(\frac{1}{2}\)
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
Tập hợp A gồm các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc.
A = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}
a) Trong các số 1, 2, 3, 4, 5, 6, có hai số là hợp số là: 4, 6.
Vậy có hai kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là hợp số” là: mặt 4 chấm, mặt 6 chấm (lấy ra từ tập hợp A = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}).
b) Trong các số 1, 2, 3, 4, 5, 6, có hai số chia 3 dư 1 là: 1, 4.
Vậy có hai kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là số chia 3 dư 1” là: mặt 1 chấm, mặt 4 chấm (lấy ra từ tập hợp A = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}).
c) Trong các số 1, 2, 3, 4, 5, 6, có ba số là ước của 4 là: 1, 2, 4.
Vậy có ba kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là ước của 4” là: mặt 1 chấm, mặt 2 chấm, mặt 4 chấm (lấy ra từ tập hợp A = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}).
6 tháng 3 2023
a: giả sử omega là ko gian mẫu của phép thử T
Nếu \(A\subset\Omega\) thì A được gọi là biến cố của T
c: Giả sử A là biến cố liên quan đến phép thử T và phép thử T có một số hữu hạn kết quả có thể có, đồng khả năng. Khi đó ta gọi tỉ số n(A)/n(Ω) là xác suất của biến cố A
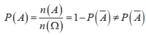
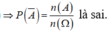
Số kết quả thuận lợi cho biến cố \(A \cup B\) là \(5 + 12 = 17\).
\(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{5}{{n\left( \Omega \right)}};P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega\right)}} = \frac{{12}}{{n\left( \Omega\right)}};P\left( {A \cup B} \right) = \frac{{n\left( {A \cup B} \right)}}{{n\left( \Omega\right)}} = \frac{{17}}{{n\left( \Omega\right)}}\)
\( \Rightarrow P\left( A \right) + P\left( B \right) = P\left( {A \cup B} \right)\)