Xét một chuyển động có phương trình \(s = 4\cos 2\pi t.\)
a) Tìm vận tốc tức thời của chuyển động tại thời điểm t.
b) Tính gia tốc tức thời tại thời điểm t.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Phương trình vận tốc là: v(t) = \(3t^2-6t+8\)
Phương trình gia tốc là: a(t) = \(6t-6\)
Thay t = 3 vào phương trình, ta được:
s = \(3^3-3\cdot3^3+8\cdot3+1=25\left(m\right)\)
\(v=3\cdot3^2-6\cdot3+8=17\left(m/s\right)\\ s=6\cdot3-6=12\left(m/s^2\right)\)
b, Theo đề bài, ta có:
\(t^3-3t^2+8t+1=7\\ \Leftrightarrow t^3-3t^2+8t-6=0\\ \Leftrightarrow\left(t-1\right)\left(t^2-2t+6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}t=1\\t^2-2t+6=0\left(vô.nghiệm\right)\end{matrix}\right.\)
Khi t = 1(s), chất điểm đi được 7m
\(v=3\cdot1^2-6\cdot1+8=5\left(m/s\right)\\ a=6\cdot1-6=0\left(m/s^2\right)\)

a) Vận tốc tức thời của con lắc: \(v(t) = - 4\pi \sin \left( {\pi t - \frac{{2\pi }}{3}} \right)\)
Gia tốc tức thời của con lắc: \(a(t) = - 4{\pi ^2}\cos \left( {\pi t - \frac{{2\pi }}{3}} \right)\)
b) Tại vận tốc tức thời của con lắc bằng 0, ta có:
\( - 4\pi \sin \left( {\pi t - \frac{{2\pi }}{3}} \right) = 0 \Leftrightarrow \sin \left( {\pi t - \frac{{2\pi }}{3}} \right) = 0 \Leftrightarrow \pi t - \frac{{2\pi }}{3} = 0 \Leftrightarrow t = \frac{2}{3}\)
Với \(t = \frac{2}{3} \Rightarrow a(t) = - \,4{\pi ^2}\cos \left( {\pi .\frac{2}{3} - \frac{2}{3}\pi } \right) = - \,4{\pi ^2}\)

a) Vận tốc trung bình trong khoảng thời gian từ t đến t + Δt là:

b) Vận tốc tức thời tại thời điểm t = 5s chính là vận tốc trung bình trong khoảng thời gian (t; t + Δt) khi Δt → 0 là :
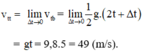

Phương trình gia tốc là: \(a\left(t\right)=v'\left(t\right)=2t+2\)
a, Tại thời điểm t = 3(s), gia tốc tức thời là: \(a\left(3\right)=2\cdot3+2=8\left(m/s^2\right)\)
b, Vận tốc của chất điểm bằng 8
\(\Rightarrow t^2+2t-8=0\\ \Leftrightarrow\left(t-2\right)\left(t+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}t=2\\t=-4\left(loại\right)\end{matrix}\right.\)
Vậy khi t = 8s thì chất điểm đạt vận tốc 8m/s.
a) Ta có \(v = s' = - 4.2\pi \sin 2\pi t = - 8\pi \sin 2\pi t\)
Vậy vận tốc tức thời của chuyển động tại thời điểm t là \( - 8\pi \sin 2\pi t\)
b) \(a\left( t \right) = v'\left( t \right) = {\left( { - 8\pi \sin 2\pi t} \right)^,} = - 8\pi .2\pi \cos 2\pi t = - 16{\pi ^2}\cos 2\pi t\)