...
Đọc tiếp
A=x2−2x+3 khi ∣�∣=0,5∣x∣=0,5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 9 2021
\(1,\\ a,A=4x^2\left(-3x^2+1\right)+6x^2\left(2x^2-1\right)+x^2\\ A=-12x^4+4x^2+12x^2-6x^2+x^2=-x^2=-\left(-1\right)^2=-1\\ b,B=x^2\left(-2y^3-2y^2+1\right)-2y^2\left(x^2y+x^2\right)\\ B=-2x^2y^3-2x^2y^2+x^2-2x^2y^3-2x^2y^2\\ B=-4x^2y^3-4x^2y^2+x^2\\ B=-4\left(0,5\right)^2\left(-\dfrac{1}{2}\right)^3-4\left(0,5\right)^2\left(-\dfrac{1}{2}\right)^2+\left(0,5\right)^2\\ B=\dfrac{1}{8}-\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{8}\)
9 tháng 9 2021
\(2,\\ a,\Leftrightarrow10x-16-12x+15=12x-16+11\\ \Leftrightarrow-14x=-4\\ \Leftrightarrow x=\dfrac{2}{7}\\ b,\Leftrightarrow12x^2-4x^3+3x^3-12x^2=8\\ \Leftrightarrow-x^3=8=-2^3\\ \Leftrightarrow x=2\\ c,\Leftrightarrow4x^2\left(4x-2\right)-x^3+8x^2=15\\ \Leftrightarrow16x^3-8x^2-x^3+8x^2=15\\ \Leftrightarrow15x^3=15\\ \Leftrightarrow x^3=1\Leftrightarrow x=1\)
19 tháng 12 2021
g: \(\Leftrightarrow\left(x^2+6x+5\right)\left(x^2+6x+8\right)-4=0\)
\(\Leftrightarrow\left(x^2+6x\right)^2+13\left(x^2+6x\right)+36=0\)
\(\Leftrightarrow\left(x+3\right)^2\left(x^2+6x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=\sqrt{5}-3\\x=-\sqrt{5}-3\end{matrix}\right.\)
25 tháng 3 2023
a: \(M=\dfrac{x^2+2x+1-x^2-3}{2\left(x-1\right)\left(x+1\right)}=\dfrac{2\left(x-1\right)}{2\left(x-1\right)\left(x+1\right)}=\dfrac{1}{x+1}\)
b: x thuộc {0;0,5}
=>x=0 hoặc x=0,5
Khi x=0 thì M=1/0+1=1
Khi x=0,5 thì M=1/0,5+1=1/1,5=2/3
=>M min=2/3 và M max=1
PT
1
CM
18 tháng 8 2018
Vẽ đồ thị hàm số
| x | -2 | -1 | 0 | 1 | 2 |
| y = 0,5 x 2 | 2 | 0,5 | 0 | 0,5 | 2 |
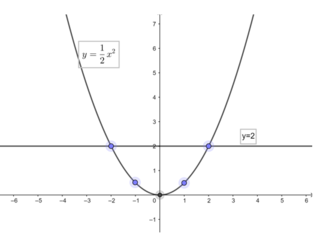
Dựa vào đồ thị ta thấy:
Khi x ≤ 2 thì y ≥ 0
PT
1
CM
28 tháng 1 2018
Vẽ đồ thị hàm số
| x | -2 | -1 | 0 | 1 | 2 |
| y = 0,5 x 2 | 2 | 0,5 | 0 | 0,5 | 2 |
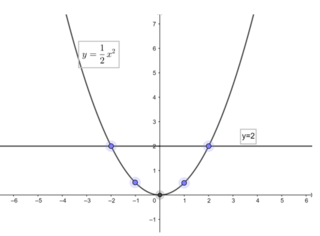
Dựa vào đồ thị ta thấy:
Khi x ≤ 0 thì y ≥ 0
PT
1
CM
21 tháng 11 2017
Vẽ đồ thị hàm số
| x | -2 | -1 | 0 | 1 | 2 |
| y = 0,5 x 2 | 2 | 0,5 | 0 | 0,5 | 2 |
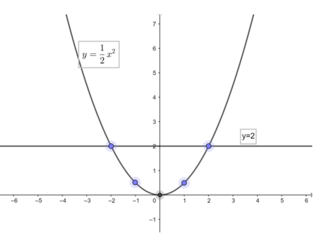
Dựa vào đồ thị ta thấy:
Khi -2 < x < 2 thì 0 ≤ y ≤ 2
15 tháng 7 2021
a) 6x(5x + 3) + 3x(1 – 10x) = 7
⇒ 30x2+18x+3x-30x2=7
⇒21x=7
⇒x=\(\dfrac{7}{21}\)
⇒x= \(\dfrac{1}{3}\)
15 tháng 7 2021
b) (3x – 3)(5 – 21x) + (7x + 4)(9x – 5) = 44
⇒15x-63x2-15+63x + 63x2-35x+36x-20=44
⇒79x-35=44
⇒79x=44+35
⇒79x=79
⇒x=1
16 tháng 6 2017
Bài 1:\(\left|2x-1\right|=2x-1\) khi \(x>0\)
b)\(\left|0,5-3x\right|=3x-0.5\) khi x= 4
c)\(\left|5x+1\right|-10x=0,5\) khi x= 0,1
Bài 2:Min A=0
Min B=-2
16 tháng 6 2017
Bài 1:
a, \(\left|2x-1\right|=2x-1\)
+) Xét \(x\ge\dfrac{1}{2}\) ta có:
\(2x-1=2x-1\)
\(\Rightarrow x\) tùy ý với \(x\ge\dfrac{1}{2}\)
+) Xét \(x< \dfrac{1}{2}\) ta có:
\(1-2x=2x-1\)
\(\Rightarrow4x=2\)
\(\Rightarrow x=\dfrac{1}{2}\) ( không t/m )
Vậy...
b, \(\left|0,5-3x\right|=3x-0,5\)
+) Xét \(x\ge\dfrac{1}{6}\) ta có:
\(0,5-3x=3x-0,5\)
\(\Rightarrow6x=1\)
\(\Rightarrow x=\dfrac{1}{6}\) ( t/m )
+) Xét \(x< \dfrac{1}{6}\) ta có:
\(3x-0,5=3x-0,5\)
\(\Rightarrow x\) tùy ý với \(x< \dfrac{1}{6}\)
Vậy \(x\le\dfrac{1}{6}\)
c, \(\left|5x+1\right|-10x=0,5\)
+) Xét \(x\ge\dfrac{-1}{5}\) ta có:
\(5x+1-10x=0,5\)
\(\Rightarrow-5x=-0,5\)
\(\Rightarrow x=\dfrac{1}{10}\) ( t/m )
+) Xét \(x< \dfrac{-1}{5}\) ta có:
\(-5x-1-10x=0,5\)
\(\Rightarrow-15x=1,5\)
\(\Rightarrow x=\dfrac{-1}{10}\) ( không t/m )
Vậy \(x=\dfrac{1}{10}\)
Bài 2:
a, Ta có: \(-\left|x-3,5\right|\le0\)
\(\Rightarrow A=0,5-\left|x-3,5\right|\le3,5\)
Dấu " = " xảy ra khi \(-\left|x-3,5\right|=0\Rightarrow x=3,5\)
Vậy \(MIN_A=0,5\) khi x = 3,5
b, Ta có: \(-\left|1,4-x\right|\le0\)
\(\Rightarrow B=-\left|1,4-x\right|-2\le-2\)
Dấu " = " xảy ra khi \(-\left|1,4-x\right|=0\Rightarrow x=1,4\)
Vậy \(MIN_B=-2\) khi \(x=1,4\)
A = \(x\) - 2\(x\) + 3
A = - \(x\) + 3
|\(x\)| = 0,5
\(\left[{}\begin{matrix}x=0,5\\x=-0,5\end{matrix}\right.\)
Thay \(x=0,5\) vào A ta có: A = -0,5 + 3 = 2,5
Thay \(x\) = -,05 vào A ta có: A = -(-0,5) + 3 = 3,5