Tính giá trị biểu thức
C= x^4 - 25x^3 + 25x^2 - 25x + 30 với x = 24
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(M=x^{10}-25x^9+25x^8-25x^7+...-25x^3+25x^2-25x+25\)
Ta thấy : \(x=24\Rightarrow x+1=25\)
\(\Rightarrow M=x^{10}-\left(x+1\right)x^9+\left(x+1\right)x^8-\left(x+1\right)x^7+...-\left(x+1\right)x^3+\left(x+1\right)x^2-\left(x+1\right)x+\left(x+1\right)\)
\(M=x^{10}-x^{10}-x^9+x^9+x^8-x^8-x^7+...-x^4-x^3+x^3+x^2-x^2-x+x+1\)
\(\Rightarrow M=1\)
Vậy \(M=1\left(tạix=24\right)\)
M=x
10
−25x
9
+25x
8
−25x
7
+...−25x
3
+25x
2
−25x+25
Ta thấy :
x
=
24
⇒
x
+
1
=
25
x=24⇒x+1=25
⇒
M
=
x
10
−
(
x
+
1
)
x
9
+
(
x
+
1
)
x
8
−
(
x
+
1
)
x
7
+
.
.
.
−
(
x
+
1
)
x
3
+
(
x
+
1
)
x
2
−
(
x
+
1
)
x
+
(
x
+
1
)
⇒M=x
10
−(x+1)x
9
+(x+1)x
8
−(x+1)x
7
+...−(x+1)x
3
+(x+1)x
2
−(x+1)x+(x+1)
M
=
x
10
−
x
10
−
x
9
+
x
9
+
x
8
−
x
8
−
x
7
+
.
.
.
−
x
4
−
x
3
+
x
3
+
x
2
−
x
2
−
x
+
x
+
1
M=x
10
−x
10
−x
9
+x
9
+x
8
−x
8
−x
7
+...−x
4
−x
3
+x
3
+x
2
−x
2
−x+x+1
⇒
M
=
1
⇒M=1
Vậy
M
=
1
(
t
ạ
i
x
=
24
)
M=1(tạix=24)


1) \(4-25x^2=0\)
\(\Rightarrow\left(2-5x\right)\left(2+5x\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}5x=2\\5x=-2\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{5}\\x=-\dfrac{2}{5}\end{matrix}\right.\)
2) Tính thì phải cho giá trị của x.
\(A=x^3-3x^2+3x-1\)
\(=\left(x-1\right)^3\)
\(=\left[{}\begin{matrix}\left(\dfrac{5}{2}-1\right)^3=\dfrac{27}{8}\\\left(-\dfrac{5}{2}-1\right)^3=-\dfrac{343}{8}\end{matrix}\right.\)

a) Với x = 24
=> x + 1 = 24 (1)
Thay (1) vào A ta được:
\(A=x^{10}-\left(x+1\right)x^9+\left(x+1\right)x^8-\left(x+1\right)x^7+...+\left(x+1\right)x^2-\left(x+1\right)x+x+1\)
\(A=x^{10}-x^{10}-x^9+x^9+x^8-x^8-x^7+...+x^3+x^2-x^2-x+x+1\)
\(A=1\)
b) Với x = 31
=> x - 1 = 30 (1)
Thay (1) vào B ta được
\(B=x^3-\left(x-1\right)x^2-\left(x-1\right)x+1\)
\(B=x^3-x^3+x^2-x^2+x+1\)
\(B=x+1\)
\(B=31+1=32\)
c) Với x = 14
=> x + 1 = 15
x + 2 = 16
2x + 1 = 29
x - 1 = 13
Thay tất cả biểu thức trên vào C ta được
\(C=x^5-\left(x+1\right)x^4+\left(x+2\right)x^3-\left(2x+1\right)x^2+\left(x-1\right)x\)
\(C=x^5-x^5-x^4+x^4+2x^3-2x^3-x^2+x^2-x\)
\(C=-x\)
\(C=-14\)
d) Ta có:
\(\left(-2+x^2\right)\left(-2+x^2\right)\left(-2+x^2\right)\left(-2+x^2\right)\left(-2+x^2\right)=1\)
\(\Rightarrow\left(-2+x^2\right)^5=1\)
\(\Rightarrow-2+x^2=1\)
\(\Rightarrow x^2=1+2=3\)
\(\Rightarrow\left[{}\begin{matrix}x=\sqrt{3}\\=-\sqrt{3}\end{matrix}\right.\)

x=-24
=>-x=24
=>-x+1=25
thay -x+1=25 vào E ta được:
E=x20+(-x+1)x19+(-x+1)x18+(-x+1)x17+...+(-x+1)x3+(-x+1)x2+(-x+1)x+(-x+1)
=x20-x20+x19-x19+x18-x18+x17-...-x4+x3-x3+x2-x2+x-x+1
=1
Vậy với x=-24 thì E=1
x = ‐24
=> ‐ X = 24
=> ‐ X + 1 = 25
thay ‐x+1=25 vào E ta được:
E = x 20 + ﴾‐ x + 1﴿ x 19 + ﴾‐ x + 1﴿ x 18 + ﴾‐ x + 1﴿ x 17 + ... + ﴾‐ x + 1﴿ x 3 + ﴾‐ x + 1 ﴿ x 2 + ﴾‐ x + 1﴿ x + ﴾‐ x + 1﴿
= x 20 ‐x 20 + x 19 ‐x 19 + x 1 8 ‐x 18 + x 17 ‐...‐ x 4 + x 3 ‐x 3 + x 2 ‐x 2 + x‐x + 1
= 1
Vậy với x=‐24 thì E=1
Học tốt nha Nguyễn Quang Linh

Lời giải:
$M=(x^{10}-24x^9)-(x^9-24x^8)+(x^8-24x^7)-(x^7-24x^6)+(x^6-24x^5)-(x^5-24x^4)+(x^4-24x^3)-(x^3-24x^2)+(x^2-24x)-(x-24)+1$
$=x^9(x-24)-x^8(x-24)+x^7(x-24)-.....+x(x-24)-(x-24)+1$
$=(x-24)(x^9-x^8+x^7-...+x-1)+1$
$=0.(x^9-x^8+....+x-1)+1=1$

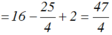
x=24 nên x+1=25
C=x^4-x^3(x+1)+x^2(x+1)-x(x+1)+30
=x^4-x^4-x^3+x^3+x^2-x^2-x+30
=-x+30
=30-24
=6