K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 4 2017
|
n |
t |
∆ti |
∆t’ |
|
1 |
0,398 |
0,006 |
|
|
2 |
0,399 |
0,005 |
|
|
3 |
0,408 |
0,004 |
|
|
4 |
0,410 |
0,006 |
|
|
5 |
0,406 |
0,002 |
|
|
6 |
0,405 |
0,001 |
|
|
7 |
0,402 |
0,002 |
|
|
Trung bình |
0,404 |
0,004 |
0,001 |
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
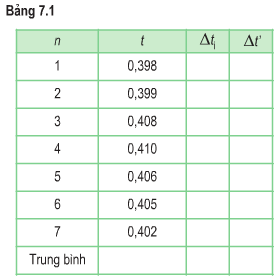
Ta có giá trị trung bình:
\(\overline x = \frac{0,398 + 0,399 + 0,408 + 0,410 + 0,406 + 0,405 + 0,402}{7}\)
\( = 0,404\)
Ta có bảng sau:
Giá trị | Độ lệch | Bình phương độ lệch |
0,398 | 0,006 | \(3,{6.10^{ - 5}}\) |
0,399 | 0,005 | \(2,{5.10^{ - 5}}\) |
0,408 | 0,004 | \(1,{6.10^{ - 5}}\) |
0,410 | 0,006 | \(3,{6.10^{ - 5}}\) |
0,406 | 0,002 | \(0,{4.10^{ - 5}}\) |
0,405 | 0,001 | \(0,{1.10^{ - 5}}\) |
0,402 | 0,002 | \(0,{4.10^{ - 5}}\) |
Tổng | \(12,{2.10^{ - 5}}\) |
Phương sai:
\({s^2} = \frac{{12,{{2.10}^{ - 5}}}}{7} \approx 0,000017\)
Độ lệch chuẩn: \(s = \sqrt {{s^2}} \approx 4,{17.10^{ - 3}}\)
Phép đo có độ chính xác cao.
VT
1 tháng 8 2019
Chọn đáp án C
Giá trị trung bình:
T ¯ = 2 , 01 + 2 , 12 + 1 , 99 3 = 2 , 04 s .
Trung bình sai lệch:
( 2 , 04 − 2 , 01 ) + ( 2 , 04 − 1 , 99 ) + 2 , 04 − 2 , 12 3
= 0 , 05 ( s ) .
Suy ra T = (2,04 ± 0,05) s.
VT
15 tháng 12 2018
Đáp án D
Ta có:
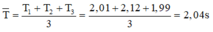
Lại có thêm:
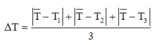
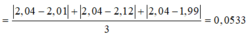
Vì tính thêm cả thang chia nhỏ nhất của đồng hồ nên ta sẽ có:
VT
20 tháng 12 2017
Đáp án D
Ta có:
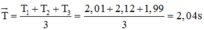
Lại có thêm:
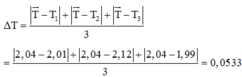
Vì tính thêm cả thang chia nhỏ nhất của đồng hồ nên ta sẽ có: 
STUDY TIP
Áp dụng công thức tính trung bình sẵn có đối với từng
VT
21 tháng 7 2019
Đáp án D
Ta có: T ¯ = T 1 + T 2 + T 3 3 = 2 , 01 + 2 , 12 + 1 , 99 3 = 2 , 04 s
Lại có thêm: Δ T = T ¯ − T 1 + T ¯ − T 2 + T ¯ − T 3 3 = 2 , 04 − 2 , 01 + 2 , 04 − 2 , 12 + 2 , 04 − 1 , 99 3 = 0 , 0533
Vì tính thêm cả thang chia nhỏ nhất của đồng hồ nên ta sẽ có: T = 2 , 04 ± 0 , 06 s
Để tính kết quả của phép đo thời gian rơi tự do của vật, ta cần lấy trung bình của các kết quả đo và trừ đi sai số của đồng hồ đo.
Trung bình của các kết quả đo là: (0,404 + 0,406 + 0,403) / 3 = 0,4043 s.
Sai số của đồng hồ đo là 0,001 s.
Vậy, kết quả của phép đo thời gian rơi tự do của vật được ghi là 0,4043 - 0,001 = 0,4033 s.