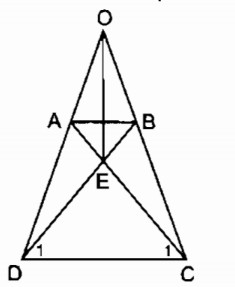
Cho hình thang cân ABCD có AB//CD.Gọi O là giao điểm của hai đường chéo và góc BOA =60 độ.Gọi E;F;M lần lượt là trung điểm của OB;OC;AD.Hãy xác định dạng của tam giác MEF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left\{{}\begin{matrix}\widehat{DAB}=\widehat{ABC}\left(hthang.cân\right)\\AD=BC\left(hthang.cân\right)\\AB.chung\end{matrix}\right.\Rightarrow\Delta ADB=\Delta BCA\left(c.g.c\right)\\ \Rightarrow\widehat{ADB}=\widehat{ACB}\Rightarrow\widehat{ADC}-\widehat{ADB}=\widehat{BCD}-\widehat{ACB}\\ \Rightarrow\widehat{OCD}=\widehat{ODC}\\ \Rightarrow\Delta COD.cân.tại.O\\ Mà.\widehat{COD}=\widehat{AOB}=60^0\Rightarrow\Delta COD.đều\)
Mà DF là trung tuyến nên cũng là đường cao
Do đó \(DF\perp AC\)
\(\Delta DFA\) có FM là trung tuyến ứng với cạnh huyền nên \(FM=\dfrac{1}{2}AD\left(1\right)\)
Cmtt \(\Rightarrow\Delta OAB.đều\Rightarrow AE\perp BD\Rightarrow EM=\dfrac{1}{2}AD\left(2\right)\)
\(\left\{{}\begin{matrix}OE=EB\\OF=FC\end{matrix}\right.\Rightarrow EF\) là đtb tam giác OBC \(\Rightarrow EF=\dfrac{1}{2}BC=\dfrac{1}{2}AD\left(hthang.cân\right)\left(3\right)\)
\(\left(1\right)\left(2\right)\left(3\right)\Rightarrow FM=EM=EF\Rightarrow\Delta MEF.đều\)

Xét ΔABD và ΔBAC có:
AB: cạnh chung
AD=BC(gt)
BD=AC(gt)
=>ΔABD=ΔBAC (c.c.c)
=>^ADB=^BCA ;
^ABD=^BAC.
=>ΔOAB cân tại O
=>OA=OB
Có: ^D=^ADB+^BDC
^C=^BCA+^ACD
Mà: ^D=^C(gt) ; ^ADB=^BCA(cmt)
=>^BDC=ACD
=>ΔODC cân tại O
=>OD=OC

a: Xét ΔABC và ΔBAD có
AB chung
BC=AD
AC=BD
=>ΔABC=ΔBAD
=>góc OBA=góc OAB
=>OA=OB
OA+OC=AC
OB+OD=BD
mà OA=OB và AC=BD
nên OC=OD
b: Xét ΔEDC có AB//DC
nên EA/AD=EB/BC
mà AD=BC
nên EA=EB
EA+AD=ED
EB+BC=EC
mà EA=EB và AD=BC
nên ED=EC
EA=EB
OA=OB
=>EO là trung trực của AB
EC=ED
OC=OD
=>EO là trung trực của CD

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

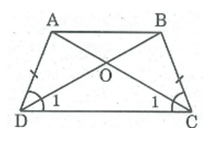
a ) Xét Δ∆ADC và Δ∆BCD, ta có:
AD = BC (tính chất hình thang cân)
∠∠(ADC) = ∠∠(BCD) (gt)
DC chung
Do đó: Δ∆ADC = Δ∆BCD (c.g.c) ⇒ ∠C1∠�1= ∠D1∠�1
Trong Δ∆OCD ta có: ∠C1∠�1= ∠D1∠�1 ⇒ Δ∆OCD cân tại O ⇒ OC = OD (1)
AC = BD (tính chất hình thang cân) ⇒ AO + OC = BO + OD (2)
Từ (1) và (2) suy ra: AO = BO.
b)
ADC=ˆBCD(gt)⇒ˆODC=ˆOCD���^=���^(��)⇒���^=���^
⇒ ∆ OCD cân tại O
⇒ OC = OD
⇒ OA + AD = OB + BC
Mà AD = BC (tính chất hình thang cân)
⇒ OA = OB
Xét ∆ ADC và ∆ BCD :
AD = BC (chứng minh trên)
AC = BD (tính chất hình thang cân)
CD cạnh chung
Do đó: ∆ ADC = ∆ BCD (c.c.c)
⇒ˆD1=ˆC1⇒�^1=�^1
⇒ ∆ EDC cân tại E
⇒ EC = ED nên E thuộc đường trung trực của CD
OC = OD nên O thuộc đường trung trực của CD
E≢ O. Vậy OE là đường trung trực của CD.
BD = AC (chứng minh trên)
⇒ EB + ED = EA + EC mà ED = EC
⇒ EB = EA nên E thuộc đường trung trực AB
E≢ O. Vậy OE là đường trung trực của AB.

Xét ΔODC có AB//DC
nên OA/AD=OB/BC
mà AD=BC
nên OA=OB
OA+AD=OD
OB+BC=OC
mà OA=OB và AD=BC
nên OD=OC
Xét ΔADC và ΔBCD có
AD=BC
DC chung
AC=BD
=>ΔADC=ΔBCD
=>góc EDC=góc ECD
=>ED=EC
OD=OC
ED=EC
=>OE là trung trực của CD
=>O,E,trung điểm của CD thẳng hàng
⎧⎪ ⎪⎨⎪ ⎪⎩ˆDAB=ˆABC(hthang.cân)AD=BC(hthang.cân)AB.chung⇒ΔADB=ΔBCA(c.g.c)⇒ˆADB=ˆACB⇒ˆADC−ˆADB=ˆBCD−ˆACB⇒ˆOCD=ˆODC⇒ΔCOD.cân.tại.OMà.ˆCOD=ˆAOB=600⇒ΔCOD.đều{DAB^=ABC^(hthang.cân)AD=BC(hthang.cân)AB.chung⇒ΔADB=ΔBCA(c.g.c)⇒ADB^=ACB^⇒ADC^−ADB^=BCD^−ACB^⇒OCD^=ODC^⇒ΔCOD.cân.tại.OMà.COD^=AOB^=600⇒ΔCOD.đều
Mà DF là trung tuyến nên cũng là đường cao
Do đó DF⊥ACDF⊥AC
ΔDFAΔDFA có FM là trung tuyến ứng với cạnh huyền nên FM=12AD(1)FM=12AD(1)
Cmtt ⇒ΔOAB.đều⇒AE⊥BD⇒EM=12AD(2)⇒ΔOAB.đều⇒AE⊥BD⇒EM=12AD(2)
{OE=EBOF=FC⇒EF{OE=EBOF=FC⇒EF là đtb tam giác OBC ⇒EF=12BC=12AD(hthang.cân)(3)⇒EF=12BC=12AD(hthang.cân)(3)
(1)(2)(3)⇒FM=EM=EF⇒ΔMEF.đều