Tam giác abc nhọn. Góc a = 60 độ . Đường cao ce và bd. Cm: Sade=1/4 Sabc
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


TA CÓ \(\Delta ADB\)đồng dạng \(\Delta AEC\)(g-g)
\(\Rightarrow\)\(\frac{AD}{AB}=\frac{AE}{AC}\)
Xét \(\Delta AED\)và \(\Delta ACB\) có :
góc A chung
\(\frac{AD}{AB}=\frac{AE}{AC}\)(CMT)
\(\Rightarrow\Delta AED\infty\Delta ACB\)(c-g-c)
\(\frac{S\Delta AED}{S\Delta ACB}=\left(\frac{AD}{AB}\right)^2\)=\(\frac{3}{4}\)
\(\Rightarrow\frac{AD}{AB}=\frac{\sqrt{3}}{2}\)
\(\Rightarrow\cos A=\frac{\sqrt{3}}{2}\)
\(\Rightarrow\)góc A=60 ĐỘ

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AB*AE;AD/AB=AE/AC
b: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
=>ΔADE đồng dạng với ΔABC
=>góc ADE=góc ABC
d: ΔADE đồng dạngvới ΔABC
=>\(\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{AD}{AB}\right)^2=\dfrac{1}{4}\)
=>\(S_{ADE}=30\left(cm^2\right)\)

A B C D E
Vì \(\widehat{BAC}=60^o\) nên \(\dfrac{AD}{AB}=\dfrac12\) (sẽ giải thích ở phần sau)
Xét tam giác ABD vuông tại D và tam giác ACE vuông tại E có:
\(\widehat{A}\) là góc chung
Nên \(\triangle ACE \backsim \triangle ABD (g.g) \text{theo tỉ số đồng dạng } k=\dfrac{AD}{AB}=\dfrac12\)
\(=> \dfrac{S_{\triangle{ADE}}}{S_{\triangle{ABC}}} = k^2=(\dfrac12)^2=\dfrac14\)
Vậy \( \dfrac{S_{\triangle{ADE}}}{S_{\triangle{ABC}}} = \dfrac14\)
Bình luận: Vì sao \(\dfrac{AD}{AB}=\dfrac12\)?
Chứng minh điều này như sau:
Kẻ đường trung tuyến DM của tam giác ABD.
Từ đây suy ra \(MD=\dfrac12 AB\) (định lý đường trung tuyến trong tam giác vuông)
Mà \(AM=\dfrac12 AB\) (do DM là trung tuyến)
Nên \(AM=MD\)
Do đó tam giác AMD cân tại M
Mà \(\widehat{MAD}=60^o\) (do \(\widehat{BAC}=60^o\))
Nên tam giác AMD đều
\(=>AM=AD\)
\(=>\dfrac{1}{2}AB=AD\) (DM trung tuyến)
\(=>\dfrac{AD}{AB}=\dfrac{1}{2}=>đpcm\)
Vì \(\widehat{BAC}=60^o\) nên \(\dfrac{AD}{AB}=\dfrac12\) (sẽ giải thích ở phần sau)
Xét tam giác ABD vuông tại D và tam giác ACE vuông tại E có:
\(\widehat{A}\) là góc chung
Nên \(\triangle ACE \backsim \triangle ABD (g.g)\)
Từ đó tự suy ra \(\triangle ADE \backsim \triangle ABC (c.g.c) \text{ theo tỉ số đồng dạng }k=\dfrac{AD}{AB}=\dfrac12\)
\(=> \dfrac{S_{\triangle{ADE}}}{S_{\triangle{ABC}}} = k^2=(\dfrac12)^2=\dfrac14\)
Vậy \( \dfrac{S_{\triangle{ADE}}}{S_{\triangle{ABC}}} = \dfrac14\)
Bình luận: Vì sao \(\dfrac{AD}{AB}=\dfrac12\)?
Chứng minh điều này như sau:
Kẻ đường trung tuyến DM của tam giác ABD.
Từ đây suy ra \(MD=\dfrac12 AB\) (định lý đường trung tuyến trong tam giác vuông)
Mà \(AM=\dfrac12 AB\) (do DM là trung tuyến)
Nên \(AM=MD\)
Do đó tam giác AMD cân tại M
Mà \(\widehat{MAD}=60^o\) (do \(\widehat{BAC}=60^o\))
Nên tam giác AMD đều
\(=>AM=AD\)
\(=>\dfrac{1}{2}AB=AD\) (DM trung tuyến)
\(=>\dfrac{AD}{AB}=\dfrac{1}{2}=>đpcm\)

a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
\(\widehat{BAD}\) chung
Do đó:ΔABD\(\sim\)ΔACE
Suy ra: AB/AC=AD/AE
hay \(AB\cdot AE=AD\cdot AC\)
b: Xét ΔADE và ΔABC có
AD/AB=AE/AC
\(\widehat{DAE}\) chung
Do đó:ΔADE\(\sim\)ΔABC
Suy ra: \(\widehat{ADE}=\widehat{ABC}\)

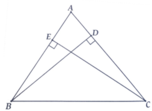
Ta có: ∆ABD ~ ∆ACE( g.g) => A D A B = A E A C
=> S A D E S A B C = A E A C 2
Mà trong ∆ACE có cosA = A E A C
=> S A D E S A B C = cos A 2
=> S A D E = S A B C . cos 2 A

Xét tứ giác BEDC có
góc BEC=góc BDC=90 độ
=>BEDC là tứ giác nội tiếp
=>góc AED=góc ACB
Xét ΔAED và ΔACB có
góc AED=góc ACB
góc A chung
=>ΔAED đồng dạng với ΔACB
=>S AED/S ACB=(AE/AC)^2=(cos60)^2=1/4
=>S AED=1/4*S ACB