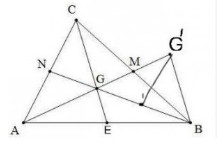
Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G’ sao cho G là trung điểm của AG’
a) So sánh các cạnh của tam giác BGG’ với các đường trung tuyến của tam giác ABC
b) So sánh các đường trung tuyến của tam giác BGG’ với các cạnh của tam giác ABC.
các bn ơi, giải đầy đủ giúp mk nha, nhanh mk sẽ tk

 AM
AM AG ( G là trọng tâm )
AG ( G là trọng tâm )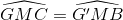
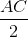
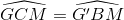 (lại góc sole trong)
(lại góc sole trong)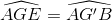 (đồng vị)
(đồng vị)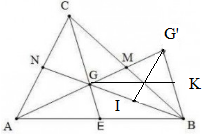
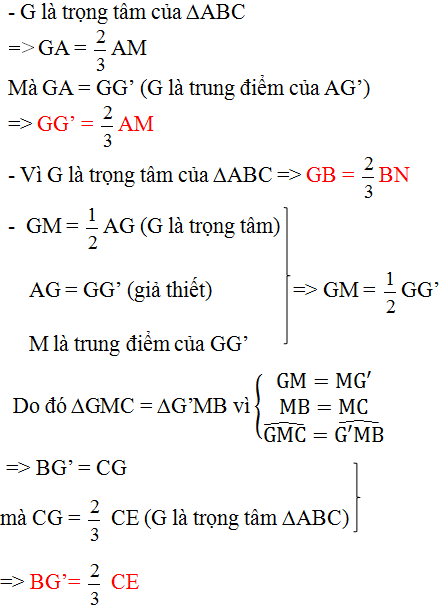


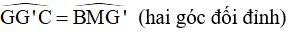
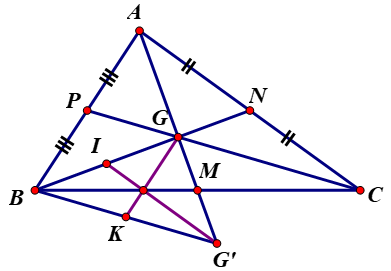
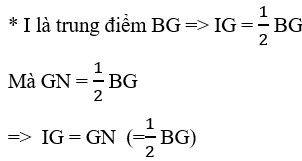
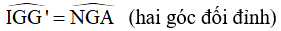
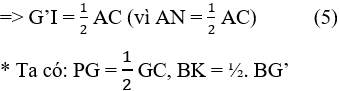

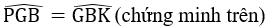
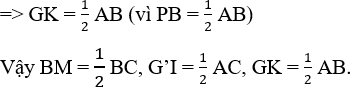
30. Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G’ sao cho G là trung điểm của AG’
a) So sánh các cạnh của tam giác BGG’ với các đường trung tuyến của tam giác ABC
b) So sánh các đường trung tuyến của tam giác BGG’ với các cạnh của tam giác ABC.
Hướng dẫn:
a) So sánh các cạnh của ∆BGG’ với các đường trung tuyến của ∆ABC BG cắt AC tại N
CG cắt AB tại E
G là trọng tâm của ∆ABC
=> GA = AM
Mà GA = GG’ ( G là trung điểm của AG ‘)
GG’ = AM
Vì G là trọng tâm của ∆ABC => GB = BN
Mặt khác : GM = AG ( G là trọng tâm )
AG = GG’ (gt)
GM = GG’
M là trung điểm GG’
Do đó ∆GMC = ∆G’MB vì :
GM = MG’
MB = MC
=> BG' = CG
mà CG = CE (G là trọng tâm ∆ABC)
=> BG' = CE
Vậy mỗi cạnh của ∆BGG' bằng đường trung tuyến của ∆ABC
b) So sánh các đường trung tuyến của ∆BGG' với cạnh ∆ABC
ta có: BM là đường trung tuyến ∆BGG'
mà M là trung điểm của BC nên BM = BC
Vì IG = BG (I là trung điểm BG)
GN = BG ( G là trọng tâm)
=> IG = GN
Do đó ∆IGG' = ∆NGA (cgc) => IG' = AN => IG' =
- Gọi K là trung điểm BG => GK là trung tuyến ∆BGG'
Vì GE = GC (G là trọng tâm ∆ABC)
=> GE = BG
mà K là trung điểm BG' => KG' = EG
Vì ∆GMC = ∆G'BM (chứng minh trên)
=> (lại góc sole trong)
=> CE // BG' => (đồng vị)
Do đó ∆AGE = ∆GG'K (cgc) => AE = GK
mà AE = AB nên GK = AB
Vậy mỗi đường trung tuyến ∆BGG' bằng một nửa cạnh của tam giác ABC song song với nó
Xem thêm tại: http://loigiaihay.com/bai-30-trang-67-sgk-toan-lop-7-tap-2-c42a5626.html#ixzz4l0rlUT9x