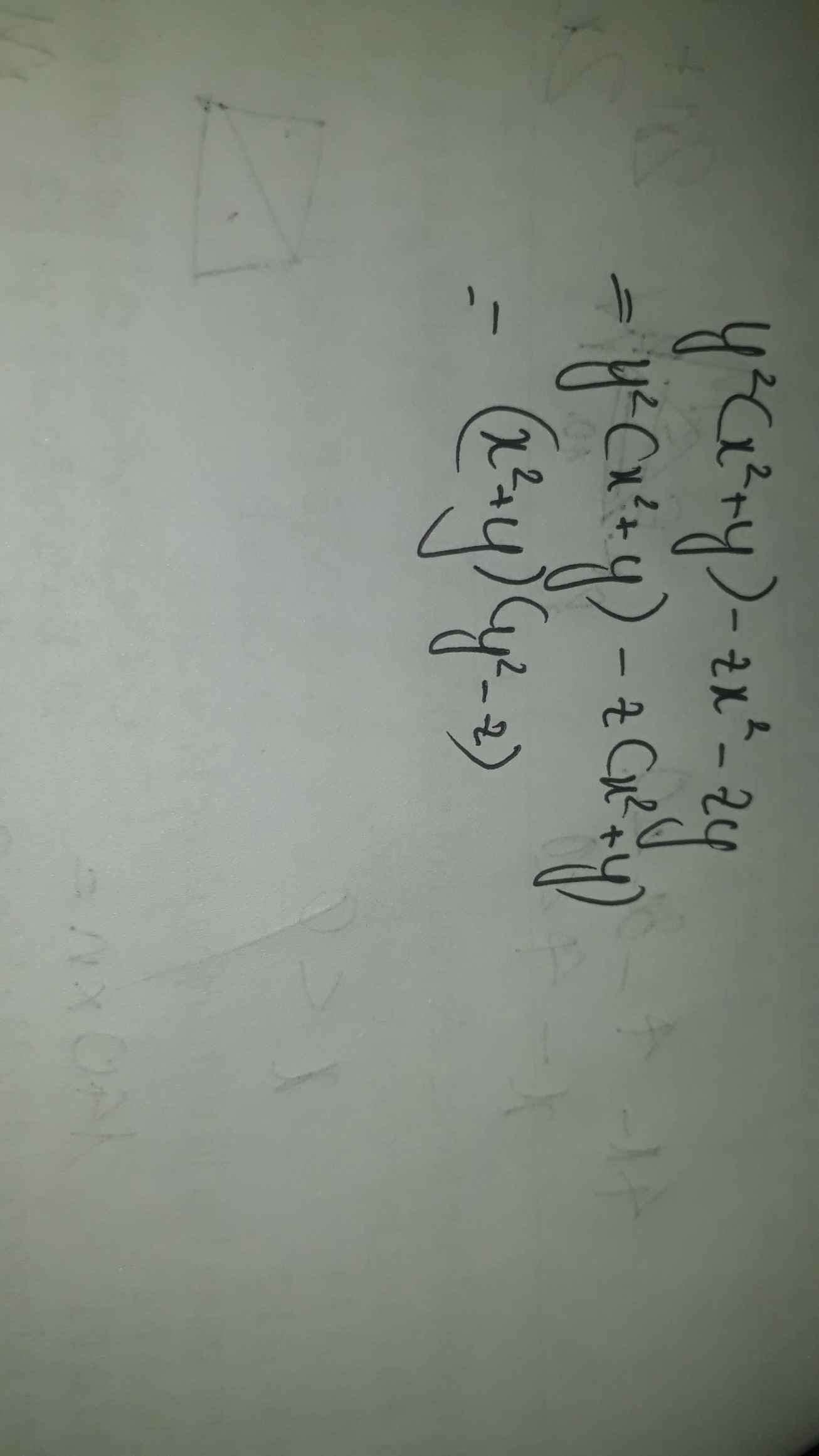Phân tích x^2+2xy+y^2-zx-zy-12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



điều kiện: x + y khác 0, z khác 0, chắc vậy :v
= \(\frac{\left(x+y\right)^2-z^2}{\left(x+y\right)^2-z\left(x+y\right)}\)
= \(\frac{\left(x+y-z\right)\left(x+y+z\right)}{\left(x+y-z\right)\left(x+y\right)}\)
= \(\frac{x+y+z}{x+y}\)

a) \(\left(5x-4\right)^2-49x^2\)
\(=\left(5x-4\right)^2-\left(7x\right)^2\)
\(=\left(12x-4\right)\left(-2x-4\right)\)
\(=-6\left(3x-1\right)\left(x+2\right)\)
c) \(x^2-y^2-x+y\)
\(=\left(x+y\right)\left(x-y\right)-\left(x-y\right)\)
\(=\left(x+y-1\right)\left(x-y\right)\)
d)\(4x^2-9y^2+4x-6y\)
\(=\left(2x-3y\right)\left(2x+3y\right)+2\left(2y-3y\right)\)
\(=\left(2x-3y\right)\left(2x+3y+2\right)\)
e) \(-x^2+5x+2xy-5y-y^2\)
\(=-\left(x^2-2xy+y^2\right)+\left(5x-5y\right)\)
\(=-\left(x-y\right)^2+5\left(x-y\right)\)
\(=\left(x-y\right)\left(y-x+5\right)\)
f) \(y^2\left(x^2+y\right)-zx^2-zy\)
\(=y^2\left(x^2+y\right)-z\left(x^2+y\right)\)
\(=\left(y^2-z\right)\left(x^2+y\right)\)

Ta có : y2( x2 + y ) - zx2 - zy
= y2( x2 + y ) - z( x2 + y )
= ( x2 + y )( y2 - z )
\(y^2\left(x^2+y\right)-zx^2-zy\)
\(=y^2\left(x^2+y\right)-z\left(x^2+y\right)\)
\(=\left(x^2+y\right)\left(y^2-z\right)\)

Ta có: \(y^2\left(x^2+y\right)-zx^2-zy\)
\(=y^2\left(x^2+y\right)-z\left(x^2+y\right)\)
\(=\left(x^2+y\right)\left(y^2-z\right)\)


a)đề sai
b)4x(x-2y)+8y(2y-x)
=4x2-8xy+16y2-8xy
=16y2-16xy+4x2
=4(4y2-4xy-x2)
=4(2y-x)2
c)3x(x+1)^2-5x^2(x+1)+7(x+1)
=(3x2+3x)(x+1)-(x+1)(5x2+7)
=(x+1)(3x2+3x-5x2+7)
=(x+1)(-2x2+3x+7)

a)\(A=3x^2+6xy+3y^2-3z^2=3\left(x^2+2xy+y^2-z^2\right)=3\left[\left(x+y\right)^2-z^2\right]=3\left(x+y-z\right)\left(x+y+z\right)\)b) \(A=\left(x+y\right)^2-2\left(x+y\right)+1=\left(x+y-1\right)^2\)
c) \(A=x^2+y^2+2xy+yz+zx=\left(x+y\right)^2+z\left(x+y\right)=\left(x+y\right)\left(x+y+z\right)\)