Tam giác ABC vuông ở A,AH vuông góc Bc.
Cho AH = 12,BC=25 tính AB,AC,BH,HC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 2 2020
A B C B H
a. Xét tam giác ABH vuông tại H, theo định lý Py-ta-go ta có:
\(^{AH^2+BH^2=AB^2\Rightarrow12^2+BH^2=15^2\Rightarrow144+BH^2=225}\)
\(\Rightarrow BH^2=225-144\Rightarrow BH^2=81\Rightarrow BH=\sqrt{81}=9\)
Vì H nằm giữa B và C \(\Rightarrow BH+HC=BC\Rightarrow9+HC=25\Rightarrow HC=25-9\Rightarrow HC=16\)
Xét tam giác AHC vuông tại H, theo định lý Py-ta-go ta có:
\(AH^2+HC^2=AC^2\Rightarrow12^2+16^2=AC^2\Rightarrow144+256=AC^2\)
\(\Rightarrow AC^2=400\Rightarrow AC=\sqrt{400}=20\)
Vậy BH = 9, HC = 16 và AC = 20.
- Bạn xem lại câu b nhé :))
28 tháng 1 2022
ABCH??20cm16 cm9 cm
Lg
*Áp dụng định lý py-ta-go ta có: (Δ AHC)
AC2=AH2+HC2
202=AH2+162
400=AH2+256
AH2=144
AH=√144 =12
*Áp dụng định lý py-ta-go ta có: (Δ AHB)
AB2=AH2+BH2
AB2=122+92
AB2=225
AB=√225 =15
1 tháng 8 2020
Sử dụng hệ thức lượng trong tam giác vuông thôi:
AB*AC = AH*BC = 12*25 = 300
AB^2 + AC^2 = BC^2 = 25^2 = 625
giải hệ trên ta được : AB = 15, AC = 20
AB^2 = BH*BC=> BH = AB^2/BC = 9
AH^2 = BH*CH=> CH = AH^2/BH = 12^2/9 = 16
NGOÀI RA HỆ PT TRÊN CÒN 1 NGHIỆM NỮA LÀ AB=20,AC=15
24 tháng 8 2021
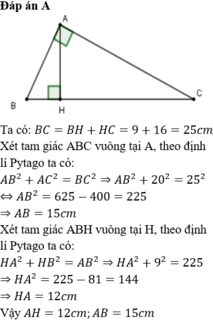
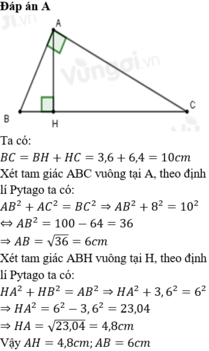
Ta có: BC=BH+HC
nên BC=3,6+6,4
hay BC=10cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AH^2=HB\cdot HC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=4,8cm\\AB=6cm\\AC=8cm\end{matrix}\right.\)
PD
cho tam giác ABC vuông cân ở A, biết AB=6cm, AC=8cm, kẻ AH vuông góc với BC tại H. Tính AH, BH và HC
0
26 tháng 9 2021
Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
TM
25 tháng 2 2021
a/
∆ABC vuông tại A, AH, vuông góc BC
=> AB.AH = HB.AC
=> AB = 15Ta có: BC^2 = AB^2 + AC^2=> BC = 25=> HB = BC - BH = 25-9 = 16
25 tháng 2 2021
a) Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AH^2+BH^2=AB^2\)
\(\Leftrightarrow AB^2=9^2+12^2=225\)
hay AB=15(cm)
Vậy: AB=15cm
Áp dụng hệ thức đường cao và hình chiếu ta có:
\(AH^2=BH\cdot HC\)
\(\Rightarrow AH^2=BH\cdot\left(BC-BH\right)\)
\(\Rightarrow12^2=BH\cdot\left(25-BH\right)\)
\(\Rightarrow144=25\cdot BH-BH^2\)
\(\Rightarrow BH^2-25\cdot BH+144=0\)
\(\Rightarrow\left(BH-9\right)\left(BH-16\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}BH=9\left(cm\right)\\BH=16\left(cm\right)\end{matrix}\right.\)
(1) Với: BH=9(cm)
\(\Rightarrow HC=BC-HB=25-9=16\left(cm\right)\)
Áp dụng hệ thức cạnh góc vuông và hình chiếu ta có:
\(AB^2=BH\cdot BC\Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{9\cdot25}=15\left(cm\right)\)
\(AC^2=HC\cdot BC\Rightarrow AC=\sqrt{HC\cdot BC}=\sqrt{16\cdot25}=20\left(cm\right)\)
(2) Với BC=16(cm)
\(\Rightarrow HC=BC-BH=25-16=9\left(cm\right)\)
Áp dụng hệ thức cạnh góc vuông và hình chiếu ta có:
\(AB^2=BH\cdot BC\Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{16\cdot25}=20\left(cm\right)\)
\(AC^2=HC\cdot BC\Rightarrow AB=\sqrt{HC\cdot BC}=\sqrt{9\cdot25}=15\left(cm\right)\)