phân tích thành nhân tử\(\left(a+1\right)\left(a+3\right)\left(a+5\right)\left(a+7\right)+15\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 4 2017
=(m+1)(m+7)*(m+3)(m+5)+15=(m+8m+7)(m+8m+15)+15
=(m+8m+11-4)(m+8m+11+4)+15=(m+8m+11)2-16+15
=(m+8m+11)2-1=(m+8m+11+1)(m+8m+11-1)=(m+8m+12)(m+8m+10)
DL
2 tháng 4 2017
(m+1)(m+3)(m+5)(m+7)+15
phân tích đa thức thành nhân tử :
(m+2)(m+6)(m\(^2\)+8m+10)
22 tháng 12 2019
(x+1)(x+3)(x+5)(x+8)+15
=[(x+1)(x+7)][(x+3)(x+5)]+15
=(x2+8x+7)(x2+8x+15)+15
Đặt t=x2+8x+7
=>x2+8x+15=t+8
=>(x2 +8x+7)(x2+8x+15)+15
=t(t+8)+15
=t2+8t+15
=t2+3t+5t+15
=t(t+3)+5(t+3)
=(t+3)(t+5)
=(x2+8x+10)(x2+8x+12)
CC
22 tháng 12 2019
Đặt \(A=\left(x+1\right)\left(x+3\right)\left(x+5\right)\left(x+7\right)+15\)
\(\Rightarrow A=\left(x+1\right)\left(x+7\right)\left(x+3\right)\left(x+5\right)+15\)
\(=\left(x^2+8x+7\right)\left(x^2+8x+15\right)+15\)
Đặt \(x^2+8x+11=t\)
\(\Rightarrow A=\left(t-4\right)\left(t+4\right)+15=t^2-16+15=t^2-1=\left(t+1\right)\left(t-1\right)\)
\(=\left(x^2+8x+11+1\right)\left(x^2+8x+11-1\right)=\left(x^2+8x+12\right)\left(x^2+8x+10\right)\)
\(=\left(x^2+2x+6x+12\right)\left(x^2+8x+10\right)\)\(=\left[x\left(x+2\right)+6\left(x+2\right)\right]\left(x^2+8x+10\right)\)
\(=\left(x+2\right)\left(x+6\right)\left(x^2+8x+10\right)\)
27 tháng 10 2017
b.\(A=\)viết lại đề nha bn
\(A=\frac{1^4+4}{3^4+4}.\frac{5^4+4}{7^4+4}...\frac{21^4+4}{23^4+4}\)
\(A=\frac{\left(4.1-3\right)^4+4}{\left(4.1-1\right)^4+4}.\frac{\left(4.2-3\right)^4+4}{\left(4.2-1\right)^4+4}...\frac{\left(4.6-3\right)^4+4}{\left(4.6-1\right)^4+4}\)
\(A=\frac{16.1^2-32.1+17}{16.1^2+1}.\frac{16.2^2-32.2+17}{16.2^2+1}....\frac{16.6^2-32.6+17}{16.6^2+1}\)
\(A=\frac{1}{17}.\frac{17}{65}.\frac{65}{145}....\frac{401}{577}=\frac{1}{577}\)
tíck mình nha bn thanks
27 tháng 10 2017
a.\(a^4+a=a\left(a^3+1\right)=a\left(a+1\right)\left(a^2-a+1\right)\)
1 tháng 10 2017
a)\(a\left(b^3-c^3\right)+b\left(c^3-a^3\right)+c\left(a^3-b^3\right)\)
\(=a\left(b^3-c^3\right)-b\text{[}\left(b^3-c^3\right)+\left(a^3-b^3\right)\text{]}+c\left(a^3-b^3\right)\)
\(=a\left(b^3-c^3\right)-b\left(b^3-c^3\right)-b\left(a^3-b^3\right)+c\left(a^3-b^3\right)\)
\(=\left(a-b\right)\left(b^3-c^3\right)-\left(b-c\right)\left(a^3-b^3\right)\)
\(=\left(a-b\right)\left(b-c\right)\left(b^2+bc+c^2\right)-\left(b-c\right)\left(a-b\right)\left(a^2+ab+b^2\right)\)
\(=\left(a-b\right)\left(b-c\right)\left(bc+c^2-a^2-ab\right)\)
\(=\left(a-b\right)\left(b-c\right)\left(c-a\right)\left(a+b+c\right)\)
XO
16 tháng 10 2020
(x - 5)2 - 4(x - 3)2 + 2(2x - 1)(x - 5) + (2x - 1)2
= [(x - 5)2 + 2(2x - 1)(x - 5) + (2x - 1)2) - [2(x - 3)]2
= (x - 5 + 2x - 1)2 - (2x - 6)2
= (3x - 6)2 - (2x - 6)2
= (3x - 6 - 2x + 6)(3x - 6 + 2x - 6) = x(5x - 12)
16 tháng 10 2020
( x - 5 )2 - 4( x - 3 )2 + 2( 2x - 1 )( x - 5 ) + ( 2x - 1 )2
= [ ( x - 5 )2 + 2( 2x - 1 )( x - 5 ) + ( 2x - 1 )2 ] - 22( x - 3 )2
= ( x - 5 + 2x - 1 )2 - ( 2x - 6 )2
= ( 3x - 6 )2 - ( 2x - 6 )2
= ( 3x - 6 - 2x + 6 )( 3x - 6 + 2x - 6 )
= x( 5x - 12 )
29 tháng 1 2023
\(a.\) \(ax^2-a^2x-x+a\)
\(=\left(ax^2-a^2x\right)-\left(x-a\right)\)
\(=ax\left(x-a\right)-\left(x-a\right)\)
\(=\left(ax-1\right)\left(x-a\right)\)
\(b.\) \(18x^3-12x^2+2x\)
\(=2x\left(9x^2-6x+1\right)\)
\(=2x\left(3x-1\right)^2\)
\(c.\) \(x^3-5x^2-4x+20\)
\(=\left(x^3-5x^2\right)-\left(4x-20\right)\)
\(=x^2\left(x-5\right)-4\left(x-5\right)\)
\(=\left(x^2-4\right)\left(x-5\right)\)
\(=\left(x-2\right)\left(x+2\right)\left(x-5\right)\)
\(d.\) \(\left(x+7\right)\left(x+15\right)+15\)
\(=x^2+15x+7x+105+15\)
\(=x^2+22x+120\)
\(=\left(x+10\right)\left(x+12\right)\)
11 tháng 10 2020
Rút gọn thôi chứ phân tích sao được ._.
( x - 3 )2 - ( 4x + 5 )2 - 9( x + 1 )2 - 6( x - 3 )( x + 1 )
= x2 - 6x + 9 - ( 16x2 + 40x + 25 ) - 9( x2 + 2x + 1 ) - 6( x2 - 2x - 3 )
= x2 - 6x + 9 - 16x2 - 40x - 25 - 9x2 - 18x - 9 - 6x2 + 12x + 18
= -30x2 - 52x - 7
11 tháng 10 2020
Sửa đề lại 1 chút là phân tích được mà bn Quỳnh:))
Ta có: \(\left(x-3\right)^2-\left(4x+5\right)^2+9\left(x+1\right)^2-6\left(x-3\right)\left(x+1\right)\)
\(=\left[\left(x-3\right)^2-6\left(x-3\right)\left(x+1\right)+9\left(x+1\right)^2\right]-\left(4x+5\right)^2\)
\(=\left(x-3-9x-9\right)^2-\left(4x+5\right)^2\)
\(=\left(8x+12\right)^2-\left(4x+5\right)^2\)
\(=\left(4x+7\right)\left(12x+17\right)\)
29 tháng 11 2023
a: \(a\left(x-y\right)-b\left(y-x\right)+c\left(x-y\right)\)
\(=a\left(x-y\right)+b\left(x-y\right)+c\left(x-y\right)\)
\(=\left(x-y\right)\left(a+b+c\right)\)
b: \(a^m-a^{m+2}\)
\(=a^m-a^m\cdot a^2\)
\(=a^m\left(1-a^2\right)\)
\(=a^m\left(1-a\right)\left(1+a\right)\)
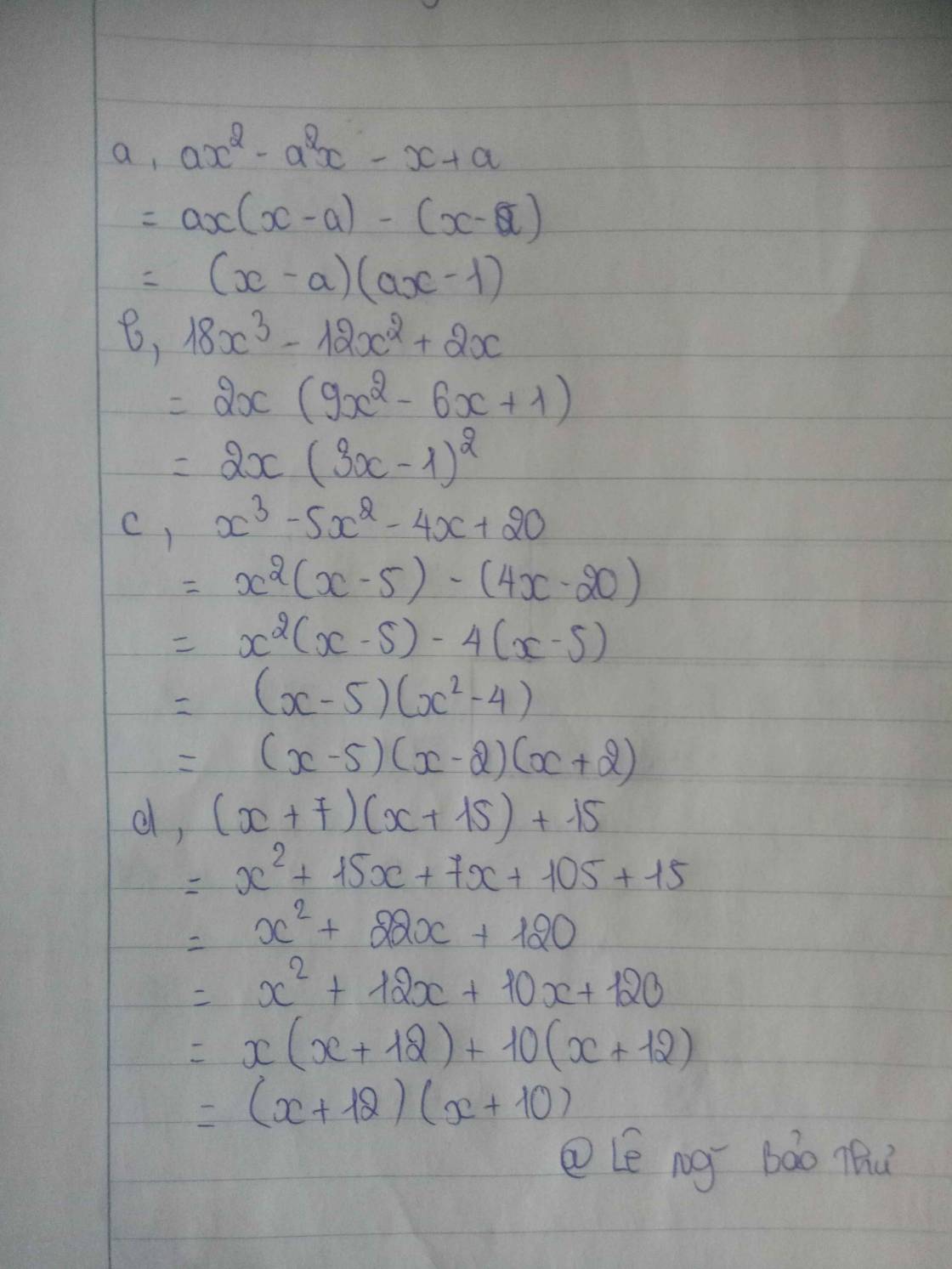
(a+1)(a+7)(a+3)(a+5)+15
=(a^2+8a+7)(a^2+8a+15)+15
=(a^2+8a+11-4)(a^2+8a+11+4)+15
=(a^2+8a+11)^2 -4^2+15
=(a^2+8a+11)^2 -1
=(a^2+8a+11-1)(a^2+8a+11+1)
=(a^2+8a+10)(a^2+8a+12)
(a+1)(a+7)(a+3)(a+5)+15
=(a^2+8a+7)(a^2+8a+15)+15
=(a^2+8a+11-4)(a^2+8a+11+4)+15
=(a^2+8a+11)^2 -4^2+15
=(a^2+8a+11)^2 -1
=(a^2+8a+11-1)(a^2+8a+11+1)
=(a^2+8a+10)(a^2+8a+12)