Xét dãy số \(\left\{x_n\right\}^{+\infty}_{n=1}\) như sau: \(x_1=1\) và với mọi \(n=1,2,...\) thì
\(x_{n+1}=\dfrac{\left(2+\cos\alpha\right)x_n+\cos^2\alpha}{\left(2-2\cos2\alpha\right)x_n+2-2\cos2\alpha}\),
trong đó \(\alpha\) là một tham số thực. Tìm tất cả các giá trị của \(\alpha\) để dãy số \(\left\{y_n\right\}\), với \(y_n=\sum\limits^n_{k=1}\dfrac{1}{2x_k+1},\forall n=1,2,...\) có giới hạn hữu hạn khi \(n\rightarrow+\infty\). Hãy tìm giới hạn của dãy số \(\left\{y_n\right\}\) trong các trường hợp đó.





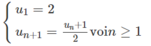

1e+84937
Ta có xn luôn dương
Ta có \(2x_n+1=\) \(2\times\dfrac{\left(2+cos\alpha\right)x_n+cos^2\alpha}{\left(2-2cos2\alpha\right)x_n+2-cos2\alpha}+1=\)
\(=\dfrac{6x_n+2cos^2\alpha+2-cos2\alpha}{\left(2-2cos2\alpha\right)x_n+2-cos2\alpha}\)
\(=\dfrac{6x_n+2cos^2\alpha+2sin^2a+1}{\left(2x_n+1\right)\left(1-cos2\alpha\right)+1}\)
\(=\dfrac{3\left(2x_n+1\right)}{2\sin^2\alpha\left(2x_n+1\right)+1}\)
\(\Rightarrow\dfrac{1}{2x_{n+1}+1}=\dfrac{2\sin^2\alpha\left(2x_n+1\right)+1}{3\left(2x_n+1\right)}\)
\(=\dfrac{1}{3}\left(2\sin^2\alpha+\dfrac{1}{2x_n+1}\right)\)
\(\Rightarrow\dfrac{1}{2x_{n+1}+1}-\sin^2\alpha=\dfrac{1}{3}\left(\dfrac{1}{2x_n+1}-\sin^2\alpha\right)\)
\(\Rightarrow\dfrac{1}{2x_{n+1}+1}-\sin^2\alpha=\left(\dfrac{1}{3}\right)^n\left(\dfrac{1}{2x_1+1}-\sin^2\alpha\right)\)
\(=\left(\dfrac{1}{3}\right)^n\left(\dfrac{1}{3}-\sin^2\alpha\right)\)
\(\Rightarrow y_n=\sum\limits^{n-1}_{i=0}\left(\dfrac{1}{3}\right)^i\left(\dfrac{1}{3}-\sin^2\alpha\right)+n\sin^2\alpha\)
\(=\dfrac{1-\left(\dfrac{1}{3}\right)^n}{1-\dfrac{1}{3}}\left(\dfrac{1}{3}-\sin^2\alpha\right)+n\sin^2\alpha\)