Cho tam giác ABC,K là trung điểm Bc,H là trung điểm AC.Cm Vecto BH,MH theo 2 vecto CA và CB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


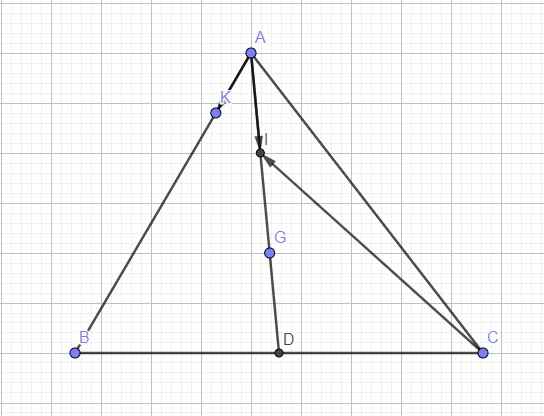
Do G là trọng tâm tam giác
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AD}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}=\dfrac{1}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CB}+\dfrac{1}{3}\overrightarrow{AC}\)
\(=\dfrac{2}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CB}=-\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\)
Do I là trung điểm AG
\(\Rightarrow\overrightarrow{AI}=\dfrac{1}{2}\overrightarrow{AG}=\dfrac{1}{2}\left(-\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\right)=-\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}\)
\(\overrightarrow{AK}=\dfrac{1}{5}\overrightarrow{AB}=\dfrac{1}{5}\left(\overrightarrow{AC}+\overrightarrow{CB}\right)=-\dfrac{1}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}\)
\(\overrightarrow{CI}=\overrightarrow{CA}+\overrightarrow{AI}=\overrightarrow{CA}-\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}=\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}\)
\(\overrightarrow{CK}=\overrightarrow{CA}+\overrightarrow{AK}=\overrightarrow{CA}-\dfrac{1}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}=\dfrac{4}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}\)

\(\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AD}\)(D là trung điểm của BC) (1)
\(\overrightarrow{AM}+\overrightarrow{AN}=2\overrightarrow{AK}\)(K là trung điểm của MN) (2)
Lấy (1) trừ (2) có: \(\left(\overrightarrow{AB}+\overrightarrow{AC}\right)-\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=2\left(\overrightarrow{AD}-\overrightarrow{AK}\right)\)
⇔\(\dfrac{\left(\overrightarrow{AB}+\overrightarrow{AC}\right)-\left(\overrightarrow{AM}+\overrightarrow{AN}\right)}{2}\)=\(\overrightarrow{KD}\)
⇔\(\dfrac{\left(\overrightarrow{AB}+\overrightarrow{AC}\right)-\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\right)}{2}\)=\(\overrightarrow{KD}\)
⇔\(\dfrac{\overrightarrow{AB}+\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AC}}{2}\)=\(\overrightarrow{KD}\)
⇔\(\dfrac{\dfrac{1}{2}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}}{2}\)=\(\overrightarrow{KD}\)
⇔\(\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)=\(\overrightarrow{KD}\)

1.
Gọi M là trung điểm BC thì theo tính chất trọng tâm: \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)\)
\(\Rightarrow\overrightarrow{AG}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\Rightarrow x+y=\dfrac{2}{3}\)
2.
\(CH=\dfrac{1}{2}BC=\dfrac{a}{2}\)
\(T=\left|\text{ }\overrightarrow{CA}-\overrightarrow{HC}\right|=\left|\overrightarrow{CA}+\overrightarrow{CH}\right|\)
\(\Rightarrow T^2=CA^2+CH^2+2\overrightarrow{CA}.\overrightarrow{CH}=a^2+\left(\dfrac{a}{2}\right)^2+2.a.\dfrac{a}{2}.cos60^0=\dfrac{7a^2}{4}\)
\(\Rightarrow T=\dfrac{a\sqrt{7}}{2}\)
3.
\(10< x< 100\Rightarrow10< 3k< 100\)
\(\Rightarrow\dfrac{10}{3}< k< \dfrac{100}{3}\Rightarrow4\le k\le33\)
\(\Rightarrow\sum x=3\left(4+5+...+33\right)=1665\)

a: \(\overrightarrow{CN}=\dfrac{1}{2}\overrightarrow{CA}+\dfrac{1}{2}\overrightarrow{CB}\)
\(=\dfrac{1}{2}\overrightarrow{CB}+\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{CB}\)
\(=\dfrac{1}{2}\overrightarrow{u}-\overrightarrow{v}\)

a: \(\overrightarrow{AI}=\dfrac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\)

\(\overrightarrow{NP}=\overrightarrow{NC}+\overrightarrow{CP}\)
\(=\dfrac{2}{3}\overrightarrow{BC}+\dfrac{1}{3}\overrightarrow{CA}\)
\(=-\dfrac{2}{3}\overrightarrow{CB}+\dfrac{1}{3}\overrightarrow{CA}\)
\(\overrightarrow{PM}=\overrightarrow{PA}+\overrightarrow{AM}\)
\(=\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{AB}\)
\(=\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{3}\left(\overrightarrow{AC}+\overrightarrow{CB}\right)\)
\(=\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\)
Ta có \(\overrightarrow{BH}=\overrightarrow{BC}+\overrightarrow{CH}=-\overrightarrow{CB}+\dfrac{1}{2}\overrightarrow{CA}\)
\(\overrightarrow{MH}=\dfrac{1}{2}\overrightarrow{BA}=\dfrac{1}{2}\left(\overrightarrow{BC}+\overrightarrow{CA}\right)=\dfrac{1}{2}\overrightarrow{CA}-\dfrac{1}{2}\overrightarrow{CB}\)