Xét tính đơn điệu (Un) với Un=4n+3/3n+4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
0
CM
21 tháng 8 2019
* Xét tử số: Ta thấy 1, 2, 3, 4, ..., n là một dãy số thuộc cấp số cộng có n số hạng với
u 1 = 1 ; d= 1 .
Tổng n số hạng của cấp số cộng: S n = u 1 + u n n 2 = 1 + n n 2 .
* Xét mẫu số: Ta thấy 1 , 3 , 3 2 , 3 3 , ... , 3 n là một dãy số thuộc cấp số nhân có n + 1 số hạng với u 1 = 1 ; q = 3
Tổng (n+ 1) số hạng của cấp số nhân: S n + 1 = u 1 . 1 − q n + 1 1 − q = 1 − 3 n + 1 1 − 3 = 3 n + 1 − 1 2 .
⇒ u n = n 3 n + 1 − 1 = n 3.3 n − 1
Bằng quy nạp ta luôn có n < 2 n , ∀ n ∈ ℕ * và 3 n > 1 , ∀ n ∈ ℕ *
⇒ u n = n 3.3 n − 1 < n 3 n < 2 n 3 n = 2 3 n
Vì lim 2 3 n = 0 nên lim u n = 0.
Chọn đáp án A
TY
1
E
20 tháng 12 2021
Ta sẽ chứng minh dãy này giảm theo quy nạp.
Với n = 1 ta có u1 = -1
Với n = 2 ta có u2 = -5
=> u1 > u2
Giả sử dãy trên đúng với uk > uk+1 tức 2k - 3k > 2(k + 1) - 3k + 1 <=> 2k - 2(k + 1) > 3k - 3k+1
Ta cần chứng minh dãy cũng đúng với uk+1 > uk+2
Hay 2(k + 1) - 3k+1 > 2(k + 2) - 3k+2
<=> 2k - 3.3k > 2(k + 1) - 3.3k+1
<=> 2k - 2(k + 1) > 3.(3k - 3k+1)
Thật vậy: Với k nguyên dương ta luôn có 3k - 3k+1 < 0 và 3 > 1 nên 3(3k - 3k+1) < 3k - 3k+1
Lại có 2k - 2(k + 1) > 3k - 3k+1 => 2k - 2(k + 1) > 3.(3k - 3k+1) (đpcm)
Vậy dãy un trên là dãy giảm
CM
24 tháng 9 2019
Chọn B.
Ta có:
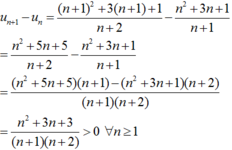
⇒ un+1 > un ∀ n ≥ 1 ⇒ dãy (un) là dãy số tăng.
un >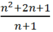 
= n + 1 ≥ 2 ⇒ dãy (un) bị chặn dưới.
CM
5 tháng 5 2017
Ta có: u n = − 5 n 1 + 4 n − 5 n − 7 n − 7 + 4.4 n − 7 n = 5 7 n ⋅ 1 + − 4 5 n − 7 + 4. − 4 7 n
Vì lim − 4 5 n = lim − 4 7 n = 0 nên lim 1 + − 4 5 n − 7 + 4. − 4 7 n = − 1 7 và lim 5 7 n = 0
Do đó lim u n = 0
Chọn đáp án D.
CM
22 tháng 7 2018
Xét tử số : 4 n 2 + 1 − 2 n = 4 n 2 + 1 − 4 n 2 4 n 2 + 1 + 2 n = 1 4 n 2 + 1 + 2 n
Xét mẫu số: 1 n 2 + 4 n + 1 − n = n 2 + 4 n + 1 + n n 2 + 4 n + 1 − n 2 = n 2 + 4 n + 1 + n 4 n + 1
⇒ l i m u n = lim n 2 + 4 n + 1 + n 4 n 2 + 1 + 2 n 2 n + 1 = lim n 2 1 + 4 n + 1 n 2 + n n 2 4 + 1 n 2 + 2 n 2 n + 1 = lim n 1 + 4 n + 1 n 2 + 1 n 4 + 1 n 2 + 2 n 2 + 1 n = lim 1 + 4 n + 1 n 2 + 1 n 4 + 1 n 2 + 2 2 + 1 n = lim 2 n 2 + 2 2 = lim 1 4 n = 0.
Do đó lim u n = 0
Chọn đáp án C
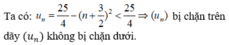
\(u_{n+1}-u_n=\dfrac{4\left(n+1\right)+3}{3\left(n+1\right)-4}-\dfrac{4n+3}{3n+4}\)
\(=\dfrac{4n+7}{3n-1}-\dfrac{4n+3}{3n+4}\)
\(=\dfrac{12n^2+16n+21n+28-12n^2+4n-9n+3}{\left(3n-1\right)\left(3n+4\right)}\)
\(=\dfrac{32n+31}{\left(3n-1\right)\left(3n+4\right)}>0\) với mọi n thuộc N*
=>(Un) là dãy tăng
Dòng đầu phải là Un+1 = 4(n+1)+3/ 3(n+1)+4 chứ ạ, s lại là 3(n+1)- 4 ạ