Vẽ đường thẳng m, lấy điểm A thuộc đường thẳng m, và điểm B không thuộc đường thẳng m. Chiều dài 15 cm và chiều rộng 12 cm. Tính chiều cao hình tam giác.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
2 tháng 11 2023
Sửa đề:
Cho tam giác MNP cân tại M, điểm Q nằm giữa M và N, lấy điểm E nằm giữa M và P sao cho MQ = PE. Từ Q kẻ đường thẳng song song MP cách NP ở F. Chứng minh:
a) Tứ giác MQFE là hình bình hành
b) Trung điểm của MF thuộc đường thẳng QE
GIẢI
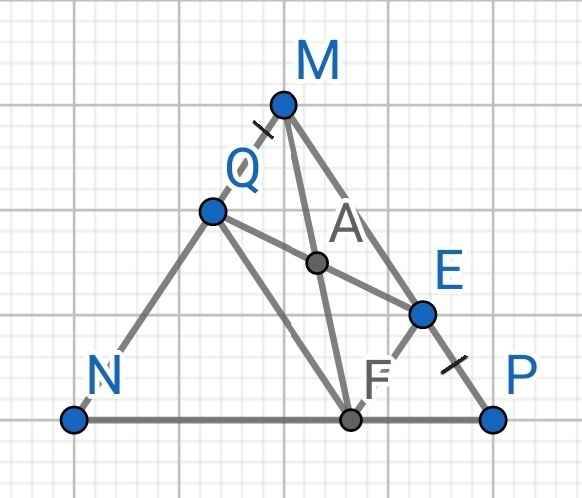
a) Do ∆MNP cân tại M (gt)
⇒ MN = MP
Mà MQ = PE (gt)
⇒ MN - MQ = MP - ME
⇒ QN = ME
Do QF // MP (gt)
⇒ ∠QFN = ∠MPN (đồng vị) (1)
Mà ∆MNP cân tại M
⇒ ∠MPN = ∠MNP
⇒ ∠MPN = ∠QNF (2)
Từ (1) và (2) ⇒ ∠QFN = ∠QNF
⇒ ∆QNF cân tại Q
⇒ QN = QF
Mà QN = ME (cmt)
⇒ QF = ME
Do QF // MP (gt)
⇒ QF // ME
Tứ giác MQFE có:
QF // ME (cmt)
QF = ME (cmt)
⇒ MQFE là hình bình hành
b) Gọi A là trung điểm của MF
Do MQFE là hình bình hành
⇒ A là trung điểm của hai đường chéo MF và QE
⇒ A là trung điểm của QE
⇒ A ∈ QE
15 tháng 12 2016
dien h hinh chu nhat ABCD la 42x18=756
dien h hinh chu nhat AMON la 756:4=189
vây NOD là 189 : 2= 94,5
đap so 94,5
5 tháng 1 2023
a: Xét tứ giác AEMF có
góc AEM=góc AFM=góc FAE=90 độ
nên AEMF là hình chữ nhật
b: \(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot4\cdot6=2\cdot6=12\left(cm^2\right)\)
28 tháng 10 2015
a) u______________M_____________O____N__________________v
các tia chung gốc M là:
Mu;Mv;MO;MN
các tia đối nhau gốc N là:
Nu và Nv ; NM và Nv; NO và Nv
các tia chùng nhau là:
Nu ;Mu;Ou
vì M và N nằm ở hai tia đối nhau chung gốc O nên O nằm giữa M và N