Rút gọc biểu thức
K
Khách
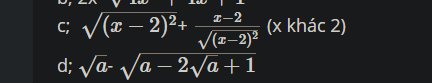
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
22 tháng 7 2016
Đề sai nha bn, mk sửa lại chút xíu ở số cuối của A là 12
A = 1002 - 992 + 982 - 972 + ... + 22 - 12
A = (100 - 99).(100 + 99) + (98 - 97).(98 + 97) + ... + (2 - 1).(2 + 1)
A = 1.(100 + 99) + 1.(98 + 97) + ... + 1.(2 + 1)
A = 100 + 99 + 98 + 97 + ... + 2 + 1
A = (100 + 1).100:2
A = 101.50
A = 5050
DY
0
17 tháng 7 2021
a) Ta có: \(P=\dfrac{15\sqrt{x}-11}{x+2\sqrt{x}-3}+\dfrac{3\sqrt{x}-2}{1-\sqrt{x}}-\dfrac{2\sqrt{x}+3}{\sqrt{x}+3}\)
\(=\dfrac{15\sqrt{x}-11-\left(3\sqrt{x}-2\right)\left(\sqrt{x}+3\right)-\left(2\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{15\sqrt{x}-11-3x-9\sqrt{x}+2\sqrt{x}+6-2x+2\sqrt{x}-3\sqrt{x}+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{-5x+7\sqrt{x}-2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{-\left(5\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{-5\sqrt{x}+2}{\sqrt{x}+3}\)
LN
1
26 tháng 12 2016
Đkxđ : \(x\ne3;-3\)
Ta có :
\(\frac{4x^2-24x+36}{x^2-9}\)
\(=\frac{4\left(x^2-6x+9\right)}{x^2-3^2}\)
\(=\frac{4\left(x^2-2.3.x+3^2\right)}{\left(x-3\right)\left(x+3\right)}\)
\(=\frac{4\left(x-3\right)^2}{\left(x-3\right)\left(x+3\right)}\)
\(=\frac{4\left(x-3\right)}{x+3}\)
HP
15 tháng 4 2021
\(A=\dfrac{\sqrt{2}.cosx-2cos\left(\dfrac{\pi}{4}+x\right)}{-\sqrt{2}.sinx+2sin\left(\dfrac{\pi}{4}+x\right)}\)
\(=\dfrac{\sqrt{2}.cosx-2\left(cos\dfrac{\pi}{4}.cosx-sin\dfrac{\pi}{4}.sinx\right)}{-\sqrt{2}.sinx+2\left(sin\dfrac{\pi}{4}.cosx+cos\dfrac{\pi}{4}.sinx\right)}\)
\(=\dfrac{\sqrt{2}.cosx-\sqrt{2}.cosx+\sqrt{2}.sinx}{-\sqrt{2}.sinx+\sqrt{2}.cosx+\sqrt{2}.sinx}\)
\(=\dfrac{\sqrt{2}.sinx}{\sqrt{2}.cosx}=tanx\)
NA
1
4 tháng 7 2015
a) \(=\left[\left(x+1\right)^2-2\left(x+1\right)\left(x-1\right)+\left(x-1\right)^2\right]-\left(x+1\right)\left(x-1\right)-2\left(x-1\right)^2=\left(x+1-x+1\right)^2-\left(x-1\right)\left(x+1+2x-2\right)\)\(=4-\left(x+1\right)\left(3x-1\right)\)
b) câu này xem lại đề đi. khó hiểu quá
HN
30 tháng 5 2017
- a/ [x/x^2-4 -2(x+2)/x^2-4 +x-2/x^2-4]:[x^2-4/x+2 +10-x^2/x+2] =(x-2x-4+x-2/x^2-4):(x^2-4+10-x^2/x+2) = - 6/x^2-4 nhân với x+2/x^2-4+10-x^2= - 6/(x+2)(x-2) nhân với x+2/6= - 1/x-2.
c/đễ A<0 <=> -1/X-2 <0 <=> x-2<0 <=>x<2
LT
2
c) \(\sqrt{\left(x-2\right)^2}+\dfrac{x-2}{\sqrt{\left(x-2\right)^2}}\)
\(=\left|x-2\right|+\dfrac{x-2}{\left|x-2\right|}\)
TH1: \(\left|x-2\right|=-\left(x-2\right)\) với \(x< 2\)
\(\Rightarrow-\left(x-2\right)+\dfrac{x-2}{-\left(x-2\right)}=-x+2-1=-x+1\)
TH2: \(\left|x-2\right|=x-2\) với \(x\ge2\)
\(\Rightarrow x-2+\dfrac{x-2}{x-2}=x-2+1=x-1\)
d) \(\sqrt{a}-\sqrt{a-2\sqrt{a}+1}\)
\(=\sqrt{a}-\sqrt{\left(\sqrt{a}\right)^2-2\cdot\sqrt{a}\cdot1-1^2}\)
\(=\sqrt{a}-\sqrt{\left(\sqrt{a}-1\right)^2}\)
\(=\sqrt{a}-\left|\sqrt{a}-1\right|\)
TH1: \(\left|\sqrt{a}-1\right|=-\left(\sqrt{a}-1\right)\) với \(a< 1\)
\(\Rightarrow\sqrt{a}-\left[-\left(\sqrt{a}-1\right)\right]=\sqrt{a}+\sqrt{a}-1=2\sqrt{a}-1\)
TH2: \(\left|\sqrt{a}-1\right|=\sqrt{a}-1\) với \(a\ge1\)
\(\Rightarrow\sqrt{a}-\left(\sqrt{a}-1\right)=\sqrt{a}-\sqrt{a}+1=1\)
\(ww\dfrac{w}{w}\)