Cho tam giác nhọn ABC cân tại A, kẻ BH vuông góc với AC tại H. Tính độ dài BC biết HA=7cm, HC= 2cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A B C H 7 cm 2 cm 2 cm
Ta có: AC = AH + HC = 7 + 2 = 9 (cm)
Vì AB = AC => AB = 9 cm
Áp dụng định lí Pi - ta - go vào t/giác AHB vuông tại H, ta có:
AB2 = AH2 + BH2
=> BH2 = AB2 - AH2 = 92 - 72 = 32
Áp dụng định lí Pi - ta - go vào t/giác AHC vuông tại H, ta có:
BC2 = BH2 + HC2 = 32 + 22 = 36
=> BC = 6 (cm)

Ta thấy: AC=AB=HA+HC+1+8=9(cm) (do ABC là tam giác cân)
Áp dụng định lý Pytago vào tam giác vuông ABH tại H, ta có:
AH2+BH2=AB2
<=>12+BH2=92
<=>1+BH2=81
<=>BH2=80(1)
<=>BH=\(4\sqrt{5}\)(cm)
Xét tam giác HBC vuông tại B. Áp dụng định lý Pytago và kết quả (1) ta có:
BH2+HC2=BC2
<=>80+82=BC2
<=>BC2=80+64=144
<=>BC=12(cm)
Vậy BC=12cm

\(\Rightarrow AC=10cm\)
\(\Rightarrow AB=10cm\) ( AB = AC )
Áp dụng định lý pitago vào tam giác vuông ABH
\(AB^2=AH^2+HB^2\)
\(\Rightarrow HB=\sqrt{AB^2-AH^2}=\sqrt{10^2-7^2}=\sqrt{51}\)
Áp dụng định lí pitago vào tam giác vuông BHC
\(BC^2=HC^2+HB^2\)
\(\Rightarrow BC=\sqrt{3^2+\sqrt{51}^2}=2\sqrt{15}\)

a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC và AH là phân giác của góc BAC
=>góc BAH=góc CAH
b: \(BH=\sqrt{5^2-4^2}=3\left(cm\right)\)
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
góc DAH=góc EAH
Do đó: ΔADH=ΔAEH
=>AD=AE
=>ΔADE cân tại A

tam giác ABC cân tại A -> AB=AC=AH+HC=5
Tam giác ABH vuông tại H.
Theo pitago: AB2=AH2+BH2 <=> BH2=AB2-AH2=52-32=16
=>BH=4
Tam giác BCH vuông tại H:
theo pitago: BC2=BH2+CH2=42+22=16+4=20
BC=\(\sqrt{20}\)
Nếu thấy hay hãy đăng ký trang youtube của mình nha: https://www.youtube.com/channel/UCdMJRiuo_35tKETQtnAYOBQ?view_as=subscriber
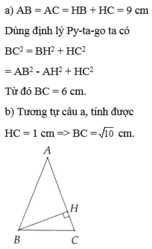

Ta có: \(AB=AC=HA+HC=7+2=9\left(cm\right)\)
Áp dụng định lí Py-ta-go vào tam giác ABH vuông tại H có:
\(BH=\sqrt{AB^2-AH^2}=\sqrt{9^2-7^2}=4\sqrt{2}\left(cm\right)\)
Áp dụng định lí Py-ta-go vào tam giác BCH vuông tại H có:
\(BC=\sqrt{BH^2+CH^2}=\sqrt{\left(4\sqrt{2}\right)^2-2^2}=2\sqrt{7}\left(cm\right)\)
cái cuối là dấu + a nhầm r
\(\sqrt{\left(4\sqrt{2}\right)^2+2^2}=6\left(cm\right)\) ạ=)