Cho biết \(a\), \(b\), \(d\) lần lượt là độ dài các cạnh và đường chéo của một hình chữ nhật. Thay dấu ? trong bảng sau bằng giá trị thích hợp.

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: Bình phương độ dài đường chéo của một hình chữ nhật là: \({5^2} + {8^2} = 25 + 64 = 89\)
Độ dài đường chéo của một hình chữ nhật là: \(\sqrt {89} = 9,43398...\)(dm)
Làm tròn kết quả này đến hàng phần mười, ta được: 9,4 dm
Chú ý: Độ dài đường chéo của một hình chữ nhật bằng căn bậc hai số học của tổng các bình phương độ dài hai cạnh của nó

Độ dài đường chéo của hình chữ nhật là:
\(\sqrt{7^2+6^2}=\sqrt{49+36}=\sqrt{85}\simeq9,2\left(dm\right)\)

Độ dài đg chéo là \(\sqrt{12^2+9^2}=15\left(cm\right)\left(pytago\right)\)

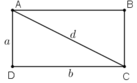
Trong hình chữ nhật ABCD ta luôn có 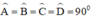
Do đó áp dụng định lý Py-ta-go ta có: d2 = a2 + b2.
Vậy :
- Cột thứ hai:
d2 = a2 + b2 = 52 + 122 = 25 + 144 = 169 nên d = 13
- Cột thứ ba:
a2 + b2 = d2 ⇒ a2 = d2 – b2 = (√10)2 – (√6)2 = 4 nên a = 2
- Cột thứ tư:
a2 + b2 = d2 ⇒ b2 = d2 – a2 = 72 – (√13)2 = 36 nên b = 6.
Vậy ta có bảng sau:
| a | 5 | 2 | √13 |
| b | 12 | √6 | 6 |
| d | 13 | √10 | 7 |
Giả sử \(ABCD\) là hình chữ nhật ; \(a\), \(b\), \(d\) lần lượt là độ dài của \(AB\), \(BC\), \(AC\)
Áp dụng định lý Pythagore vào \(\Delta ABC\) vuông tại \(B\) ta có:
\(A{C^2} = A{B^2} + B{C^2}\)
Do đó \({d^2} = {a^2} + {b^2}\) ; \({b^2} = {d^2} - {a^2}\); \({a^2} = {d^2} - {b^2}\)
Suy ra: \(d = \sqrt {{a^2} + {b^2}} \); \(b = \sqrt {{d^2} - {a^2}} \); \(a = \sqrt {{d^2} - {b^2}} \)
Với \(a = 8\); \(b = 6\) ta có: \(d = \sqrt {{8^2} + {6^2}} = \sqrt {64 + 36} = \sqrt {100} = 10\)
Với \(a = \sqrt {15} \); \(d = \sqrt {24} \) ta có: \(b = \sqrt {{{\sqrt {24} }^2} - {{\sqrt {15} }^2}} = \sqrt {24 - 15} = \sqrt 9 = 3\)
Với \(b = 5\); \(d = 13\) ta có: \(a = \sqrt {{{13}^2} - {5^2}} = \sqrt {169 - 25} = \sqrt {144} = 12\)